A Priori Probability

What is a Priori Probability?

When there are a limited number of possible outcomes, and they are equally likely to occur, the chance of an event happening is known as a priori probability. The previous result has no bearing on the events in a priori probability. Alternatively, any outcomes achieved so far will not give you a competitive advantage in forecasting future results. A priori probability is sometimes explained with a coin toss. Irrespective of whether you have a streak of heads or tails, there is a 50% chance that each coin toss will finish in either direction.

Key Takeaways

• According to a priori probability, the result of the subsequent event is independent of the result of the preceding event.
• A priori also eliminates the independent experience of consumers. You cannot predict the next result since the results are random and noncontingent.
• A coin flip is a wonderful illustration of this. Because there are two sides, the odds are always 50%, regardless of what was flipped before it or how many flips have taken place.

Understanding "A Priori Probability"

Significantly, a priori probability is a theoretical foundation for the probability that can be limited to a few possible outcomes. It is fairly simple to calculate a priori probability using the following formula:

A Priori Probability = Desired Outcome(s)/Total Number of Outcomes

Therefore, one (the intended outcome of six) divided by six is the a priori chance of throwing a six on a six-sided die. In other words, your chances of rolling a six are 16%, and your chances of rolling any other figure you pick are the same. The chances of throwing an even number (or odd number) on the same die grow to 50% just because there are other desired outcomes, as a priori probabilities can be stored within the outcome set.

Real-World Example of A Priori Probability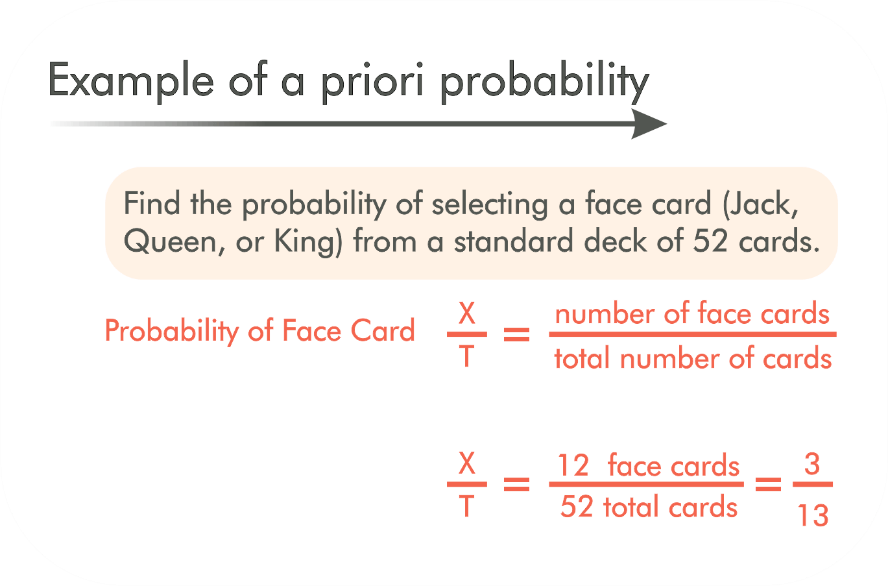

Your chances of winning a lottery based on numbers are a common example of a priori probability. Given that you can purchase multiple tickets with different number combinations and that your chances depend on the collection of numbers on the tickets being randomly picked in the right sequence, the procedure for determining the probability becomes significantly more complicated. Nevertheless, the combinations that will lead to a win are limited in number. Sadly, there are far more conceivable outcomes than desirable results based on your specific set of tickets. A jackpot like the Powerball Jackpot in the United States has a one in hundreds of millions chance of awarding the big prize. Furthermore, as the pot grows and more players participate, the likelihood of winning the big prize solely (without dividing) decreases.

A Priori Probability and Finance

There aren't too many examples of a priori probability used in finance. Most outcomes that matter to individuals in finance do not have a fixed number of possibilities. Hence it is important to discourage people from leaving their financial future in the hands of the lottery. You cannot claim that the price of bitcoin has three possible outcomes-an increase, a decrease, or a stay-the-course-when each of these outcomes is affected by a variety of external variables that alter the possibility of each one.

In contrast to classical probability, empirical or subjective probability is more frequently used in the banking industry. Empirical probability makes use of historical evidence to predict future results. In subjective probability, you use the information and your own experiences and viewpoints to make a judgment call that is particular to you. An investor may fairly anticipate a stock's current price movement to continue whether it has been on a rampage for three days and has surpassed analysts' recommendations. Another investor, seeing the same price movement and recalling how this company experienced consolidation after a sharp surge two years earlier, would interpret the same value data differently and draw the opposite conclusion. Depending on the market, neither (none of these two) investor may be any more accurate than a prediction made using a priori probability. Still, we feel much better about choices when at least some reasoning beyond random chance can support us (our theory).

A Priori Probability in Statistical Mechanics

Statistical mechanics uses the "a priori probability" extensively. The classical version is the ratio of elementary events (such as the number of instances a die is thrown) to all occurrences, as determined deductively, without any experimental data. Each elementary event is assumed to have the same probability in the case of the die if we only observe it on the table without tossing it. As a result, the chance of each result (any specific occurrence of number/face of dice) of a hypothetical toss of the (perfect) dice or simply by calculating the number of faces is 1/6.

Probability, a unit of measurement established for each elementary occurrence, states that there is an equal chance that each die face will emerge. If we roll the dice 20 times and then inquire how many instances (out of 20) the number 6 comes on the upper face, the outcome is different. In this situation, time is a factor, and the chance changes depending on how much time has passed or how many times the die has been tossed. The a priori probability, however, is independent of time. You may observe the die on the table for however long you desire without disturbing it and determine that the likelihood of the number 6 appearing on the upper face is still 1/6.