Area and Perimeter

We all must have heard of the word 'Geometry,' which is a branch of Mathematics that deals with the study of shapes, angles, structures, and methods of their measurements, such as area and perimeter; apart from these, this branch of mathematics also focuses on the spatial properties of the shapes and structures and their relative configuration in a plane. Geometry comprises two Greek words, 'Geo' and 'Metron.' The meaning of 'Geo' is 'Earth.' The meaning of 'Metron' is 'Measurement,' by considering this, we can say that Geometry is the stream of mathematics that describes the measurement (area and perimeter) of shapes, objects, planets, angles, etc.

Geometry is mainly classified into two types according to the dimensions of the shapes.

1. Two-dimensional (2-D) Geometry
2. Three-dimensional (3-D) Geometry

One basic and most important point, which is followed in both 2-D geometry as well as in 3-D geometry, is that all the shapes and structures which are studied in Geometry are formed from the points, rays, lines, and plane surfaces, and all the shapes we study in geometry are formed using lines which are intersecting at some common points and form a close structure on a plane surface; so, every shape has a definite area and perimeter.

Mathematics is a vast subject with many branches, and one of the most essential concepts in mathematics is the "Area and Perimeter" of objects. In mathematics, the area can be referred to as the measure of the two-dimensional (2-D) surface, and the perimeter can be referred to as the measure of lines of that object, such as a plane, shape, circle, etc. They are such a basic concept that they have many practical applications in various fields.

We have been listening about the concept of area and perimeter in elementary school when we used to calculate the area and perimeter of simple shapes and objects like squares and rectangles by using simple formulas. In later years, we learn about some complex shapes like circles, triangles, and regular polygons. In mathematics, the area is usually measured in square units, such as square cm, square m, and square ft, while the perimeter is measured in units, such as centimeters (cm), meters (m), and feet (ft).

There are some essential properties of the area of any object, i.e., adding the areas of two different shapes; it is beneficial when an object or shape is made up of different types of shapes, and this same condition holds for the perimeter of that object. For example, the area of an L-shaped object can be calculated by dividing that shape into two rectangular shapes and then adding their areas. Similarly, the perimeter can also be calculated by simply adding the numbers. Similarly, the area of a complex polygon can also be calculated by dividing the polygon into small rectangles and triangles and then adding their areas.

Areas and Perimeters have many different applications in the real world; for instance, the architecture uses the concept of area and perimeter to estimate the amount of material that will be used to build a structure, and they also use the area and perimeter to calculate the amount of space needed for people to move in the building.

There are so many ways to calculate the area and perimeter of an object depending on its shape and characteristics; for example, the area of a triangle can be calculated by multiplying the base and height of the triangle and dividing the result by two (2). The perimeter of the triangle can be measured simply by adding all sides. In this article, we will learn many things about the area and perimeter of different shapes.

History of Area and Perimeter

Since ancient times, "area and perimeter" has been an essential part of human history, as humans have always been interested in measuring and keeping the space around them. The area's history can be traced back to the ancient civilizations of Mesopotamia, Egypt, and India, where our ancestors developed mathematical systems for measuring land, buildings, and other physical spaces.

In ancient India, the area concept was developed as part of the mathematical tradition of the Vedic period. We all know that the first correct measure of the circumference of the Earth was measured by "Aryabhata" in the 5th century. In the famous book of "Chanakya," "Arthashastra," we learn about various measurement units used at that time, like angular, yojana, and Dhanusha. The relation between angula, yojana, and Dhanusha is given in Arthashastra, 'Angula' literally means 'finger,' which shows that in ancient India, people used to measure the length and width with the help of their body parts. By taking measures of the building of "Mohenjo-Daro," it is calculated that the average size of one angular at that time was precisely equal to 1.6764 centimeters.

In Mesopotamia, one of the earliest civilizations in the world, these people developed a system of measurement based on the length of the human body, known as the cubit. This system was used to measure length and area; in this system, one square cubit equals an area of one square foot. The Babylonians (they were also Mesopotamians) later developed a more suitable system for measurement that included units of the area, such as the aroura and the biltu, which were used to measure agricultural land.

In ancient Egypt, the concept of the area was mainly used for surveying and for measuring lands for agriculture, as fertile land was scarce. The Egyptians developed a system of measurement based on the cubit and the palm, which were used to measure both length and area. They also used a system of ropes and pegs to mark out the boundaries of fields and other land areas. As we know, the capital of Egypt, 'Cairo,' is famous for its giant pyramidal structure. Is it possible to make those structures without knowledge of the area and perimeter? The answer is no.

During the medieval period, the study of geometry and mathematics continued to evolve; with notable contributions from Islamic scholars such as Al-Khwarizmi, he developed the concept of algebra and made essential improvements (discoveries) in trigonometry. The area concept was further developed during this period, with mathematicians developing methods for calculating the area of complex shapes using principles of geometry and calculus.

In the modern era, the area concept has become central to many fields of study, including mathematics, physics, and engineering. "Isaac Newton" When we read this name, we glimpse the "Law of Gravitation," but Do you know? That the concept of integration in mathematics was developed by Isaac Newton, integration is a fundamental concept for finding the area of complex shaped objects. The development of computers and digital technology has opened a new path to finding and calculating the area of different objects. It has made it possible to apply the area concept in new and innovative ways.

Today, the area concept continues to be essential to our understanding of the world around us, from the size of buildings and cities to the measurement of ecosystems and the planet itself. As our understanding of the universe and its complexities continues to grow, the concept of the area will undoubtedly play an essential role in helping us to comprehend and quantify the vastness of space and time.

Definitions

• Area

In mathematics, especially in geometry, an area can be defined as the measure or extent of two-dimensional shapes or surfaces, simply saying that the space is covered by any object or thing on a surface (2-D).

• Perimeter

The perimeter of an object can be defined as the sum of the lengths of the outer sides; in simple words, the perimeter of any object is equal to the length of a thread rolled or tracked above the sides of that shape.

The concept of area is closely related to the perimeter, calculated by adding the length of all the sides of a shape or surface. However, while perimeter only describes the length of the boundaries of a shape or surface, area describes the amount of space enclosed within that boundary.

Units to Measure Area

We have heard about feet, meters, and Kilometers as the unit of measurement, but have we ever thought about why there is no single-unit system to measure the length of anything? It is called the SI system, and its complete form is "Systeme International," also known as the International System of Units. It is a foundation established in 1960 to make the standard units of measurement of different things worldwide.

So, to measure length, we have meter, foot, and kilometer as standard units. One meter is equal to 100 centimeters, one kilometer equals 1000 meters, and one foot is equal to 30.48 centimeters. They have different notations to represent like the short form of centimeters is cm, the short form of meter is m, the short form of a kilometer is km, and the short form of foot is ft.

• 1 ft. = 30.48 cm
• 1 m = 100 cm
• 1 km = 1000 m

Area and Perimeter of Different Shapes

Various formulas and methods for calculating the area of different shapes, such as triangles, circles, rectangles, and irregular polygons. In general, the formula for calculating the area of a shape involves multiplying a base or diameter by a height or radius or dividing the complex shape into smaller and simpler shapes or parts whose areas can be easily calculated and then adding them together. At the same time, any shape's perimeter can be calculated by simply adding all the sides of that shape. We will learn basic formulas of area and perimeter for some basic shapes.

1. Square

In mathematics, a square can be defined as a closed four-sided quadrilateral or structure with all four sides of equal length; also, all four angles are equal in measure, i.e., 90 degrees or pi / 2. A square has four vertices and therefore has two diagonals, which are also equal to each other in length. The perimeter of a square-shaped object is given by adding the length of all four sides. The area of a square-shaped object is given by the square of a side, and the perimeter is given by four times the length of a side. As shown in the image given below.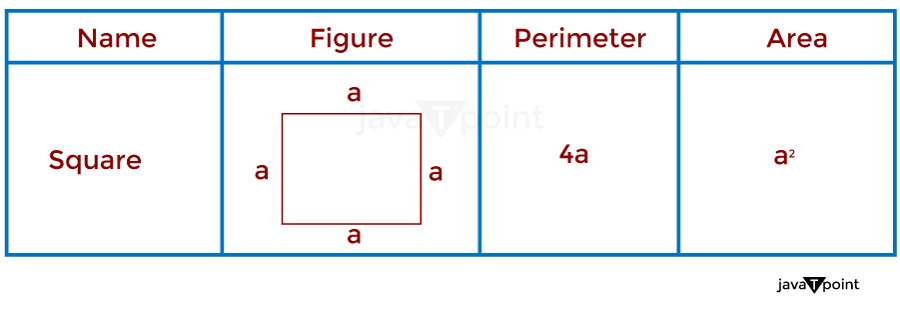

2. Rectangle

In mathematics, a rectangle can be defined as a closed four-sided quadrilateral with opposite sides of equal length; it also has angles of 90 degrees each. A rectangle has four vertices; therefore, two diagonals are equal in length. The perimeter of a rectangular-shaped object is given by adding the length of all four sides. The area of a rectangular-shaped object is given by multiplying the length and breadth of a rectangle. As shown in the image given below.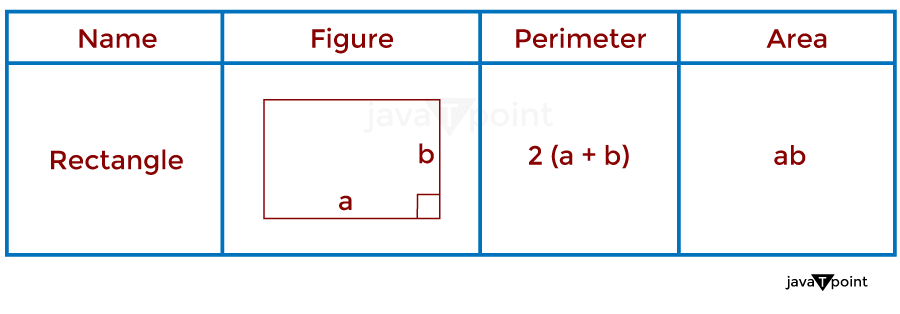

3. Triangle

The word "Triangle" can be breakdown into two parts, "tri" and "angle," which means three angles. So, based on this, a triangle can be defined as a closed three-sided structure or shape with three angles; it has three vertices, so it does not have any diagonals. The perimeter of a triangular-shaped object is given by adding the length of all three sides. The area of a triangular-shaped object is given by multiplying the base and height divided by two (2). As shown in the image below.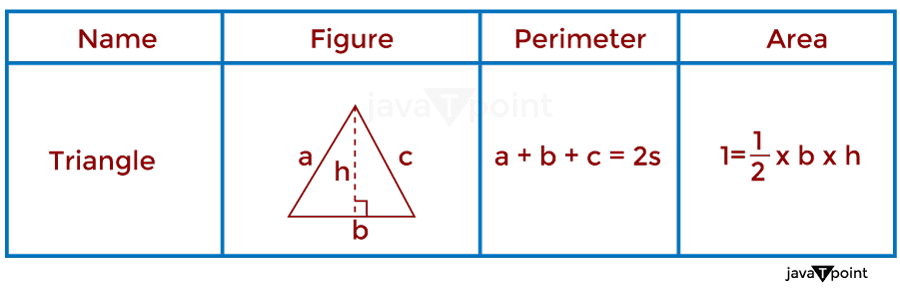

4. Right Triangle

As we can see in its name, a right-angle triangle can be defined as a triangle with one of the angles at 90 degrees. The famous Pythagoras theorem is made for this right-angled triangle. The perimeter of a triangular-shaped object is given by adding the length of all three sides. The area of a triangular-shaped object is given by multiplying the base and height divided by two (2). As shown in the image below.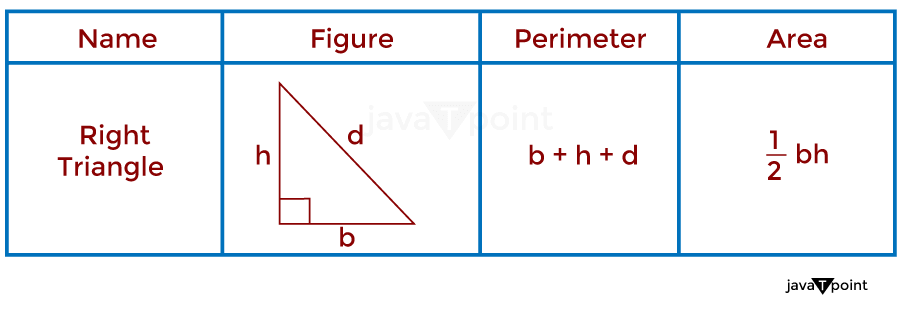

5. Equilateral Triangle

As we can see in the name of an equilateral triangle, an equilateral triangle can be defined as a triangle with all three sides of equal length; due to this equilateral triangle has all three angles in an equal measure also, i.e., 60 degrees. The perimeter of a triangular-shaped object is given by adding the length of all three sides. The area of a triangular-shaped object is given by multiplying base and height divided by two (2); it can also be determined by sqrt (3)/4 times the square of the side of an equilateral triangle. As shown in the image below.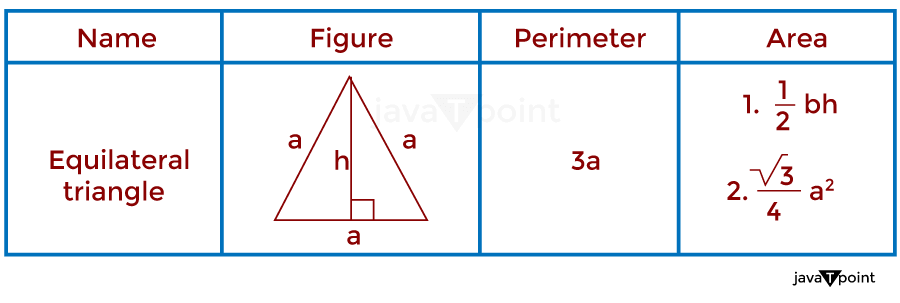

6. Isosceles Right Triangle

Isosceles can be broken down into two parts, "Iso" and "scale," which means same side; on the bases of this, an isosceles right triangle can be defined as a triangle that has two sides of equal length, and the angle between these sides is of 90 degrees. The perimeter of a triangular-shaped object is given by adding the length of all three sides. The area of a triangular-shaped object is given by multiplying the base and height divided by two (2). As shown in the image below.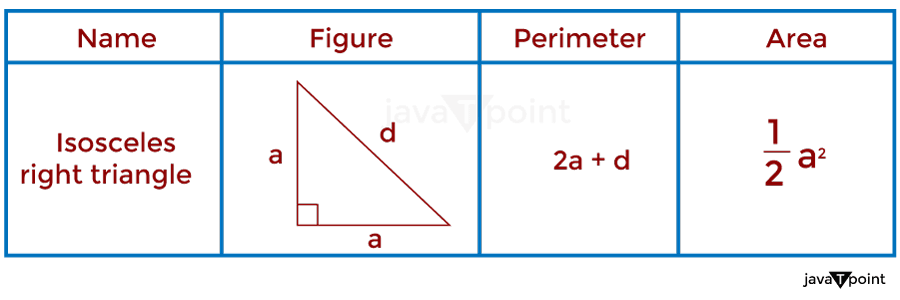

7. Circle

A circle is a two-dimensional shape or surface with no corners and no vertices, it can be defined as a path of points that are equidistant of a given point called the center of the circle, and the distance is called the circle's radius. The perimeter of a circle is given by multiple of twice the circle's radius and pi (π).

The area of a circle is given by the multiple of pi (π), and the square of the circle's radius and the circle's perimeter is given by twice the product of pi (π) and the radius. As shown in the image below: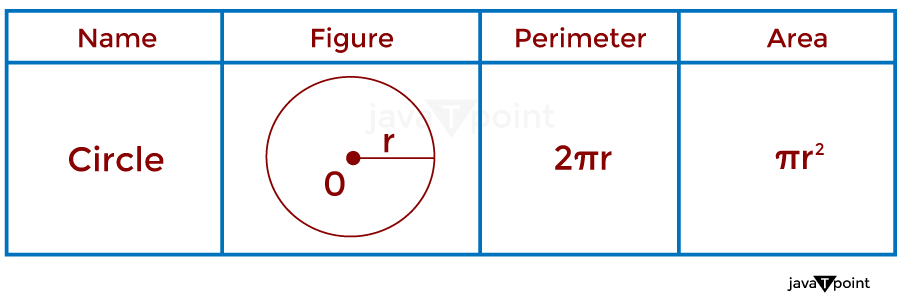

8. Rhombus

In mathematics, a Rhombus can be defined as a closed four-sided quadrilateral or shape with all four sides of equal length (same as a square), but the angles between the sides are of different measures. It has four vertices and two diagonals, which are of different lengths. So, therefore, a square is a particular case of a rhombus. The perimeter of a rhombus can be given by multiple of four and the length of a side of a rhombus. The area of a rhombus is given by multiplying the lengths of the diagonals divided by two. As shown in the image below: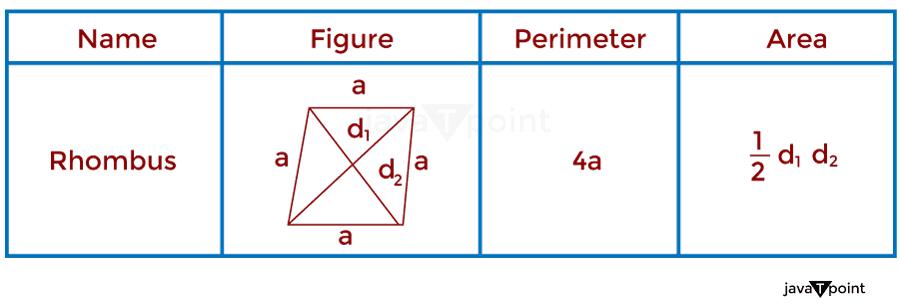

9. Parallelogram

In mathematics, a Parallelogram can be defined as a closed four-sided quadrilateral or shape with opposite sides of equal length (same as a rectangle), but the angle between the sides is of different measures. It has four vertices and therefore has two diagonals of different lengths; a rectangle is a special case of a parallelogram. Twice the sum of unparallel sides gives the perimeter of a parallelogram. Multiple heights and bases of the parallelogram give the area of a parallelogram. As shown in the image below: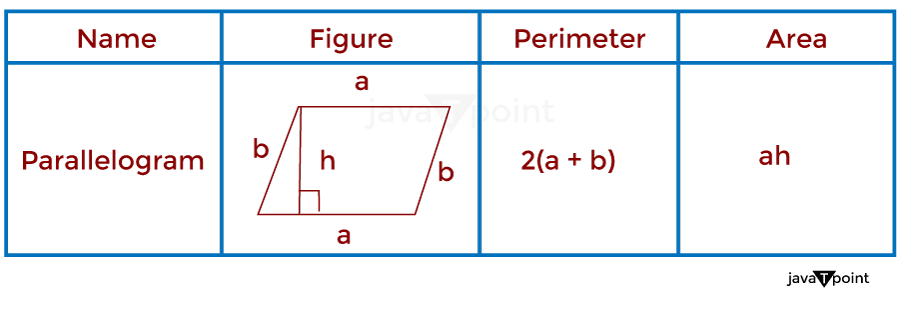

10. Trapezium

In mathematics, a trapezium can be defined as a closed four-sided quadrilateral or shape with two parallel sides opposite each other and two unparalleled sides opposite to each other. It has four vertices and therefore has two diagonals of different lengths. The perimeter of a trapezoidal-shaped object is given by adding the length of all four sides. The area of a trapezium is given by the product of the heights of the trapezium and the sum of parallel sides divided by two (2). As shown in the image below.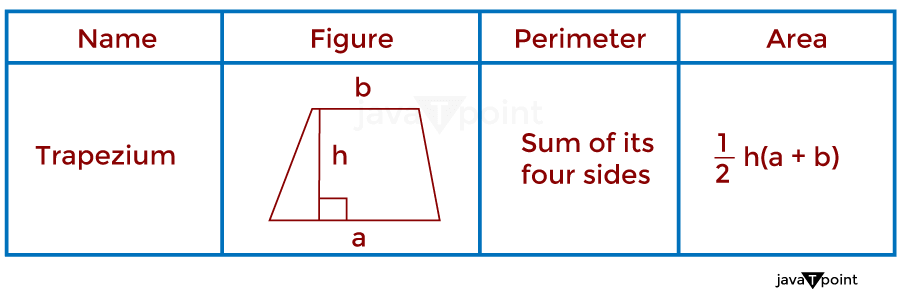

Applications

The concept of area and perimeter, which measure the size of a two-dimensional region or shape, has various applications in various fields. Here are some examples:

1. Engineering: Engineers use the concept of area and perimeter to design structures such as buildings, bridges, and roads; they also use it to calculate the cross-sectional area and perimeter of pipes, cables, and other components.
2. Mathematics: The concepts of area and perimeter are the base of geometry and trigonometry, where it is used to solve problems that involve shapes such as triangles, circles, rectangles, and polygons; calculus also uses the concept of area to find the area under a curve.
3. Agriculture: In agriculture, the concept of area and perimeter is used to determine the amount of land needed for crops and to calculate the yield per unit area.
4. Physics: The area is used in physics to calculate quantities such as the area of a cross-section of a beam, the area of a surface, and the area of a capacitor plate.
5. Cartography: Maps represent a region, and the area of a region is an essential factor in mapmaking. Cartographers use the concept of area to accurately describe (map) the size of different regions on a map in a particular proportion.
6. Architecture: Architects use the concept of area to design and plan the layout of buildings and to calculate the amount of materials needed for construction.
7. Economics: The concept of area and perimeter is used in economics to calculate the area under a demand or supply curve, which represents the total revenue or cost associated with a certain level of production.
8. Environmental Science: The concept of area is used in environmental science to calculate the size of a habitat or ecosystem, which is essential for understanding the biodiversity and health of an ecosystem.

These are just a few examples of the many applications of the area concept in various fields.

Conclusion

We can say that the concepts of area and perimeter play an essential role in geometry and various real-world applications. Area refers to the extent of a two-dimensional surface enclosed by a shape, while perimeter represents the total length of its boundary; these two measures are essential in understanding and quantifying the spatial characteristics of shapes and figures.

Throughout history, mathematicians and scientists have studied area and perimeter very briefly to unlock the secrets of the natural world and build civilizations; from ancient times to the modern era, these concepts have been used in architecture, engineering, land surveying, and many other fields. They are crucial in designing buildings, planning cities, and determining the materials needed for construction. Moreover, area and perimeter are not limited to simple shapes like squares, circles, or triangles. Advances in mathematics have enabled the calculation of these measures for complex and irregular figures, making them applicable in diverse industries like computer graphics, image processing, and geographical information systems.