What is the Sum of all Numbers from 1 to 99?

AP is a sequence of numbers in which the difference between the two consecutive numbers is a constant value. For example, the series of natural numbers 1,2,3,4,5,6,8,... . The series has a common difference, and it is . Notations are used for denoting Arithmetic Progression.

Types of Progression

In mathematics, there are three types of Progression exist, and they are:

• Harmonic Progression
• Geometric Progression
• Arithmetic Progression

Arithmetic Progression is denoted by the notation AP.

Notations

Several Notations are used in the Arithmetic Problems, and they are:

The sum of the First n terms,S_n

First Term = a

Common difference = d

First Term = (a)

nth term =a_n

These terms show the property of the Arithmetic Progression.

First Term of arithmetic progression

The AP can also be presented in the form of common differences, which are as follows.

a,a+d,a+2d,a+3d,a+4d ,....a+(n-1)d

Here the "a" represents the first Term.

a₁= a

a₂= a + d

a₃= a + 2d

The common difference in the AP

In a series, the given are common differences: the nth Term and the first Term. Suppose the Progression begins like a₁, a₂, ....a_n.

a₂-a₂= d

The common difference can be negative, zero, or positive.

The General Form of AP

Term Position = 1

Representation of terms: a₁

Value of the term = a = a + (1 - 1) d

Term Position: 2

Representation of n terms = a₂

Values of the term = a +d = a + (2-1) d

= a + d

Term Position = 3

Representation n of terms = a₃

Values of the term = a + (3 ' 1) d

= a +2d

Term Position = 4

Representation of the Term = a₄

Values of the term = a + 3d = a + (4 - 1) d

Formulas for the Arithmetic Progression

Two major formulas are used in the Arithmetic Progression, and they are related to

• The sum of the first n terms
• The nth Term of the AP

The formula for the nth Term

a_n =a+(n-1)d

Here,

a_n= nth Term

First Term = a

Common difference = d

Number of terms = n

Different Types of AP

• Finite Arithmetic Progression: The Progression that possesses a finite number of terms is called finite Arithmetic progression. A finite arithmetic progression will contain a last term.
  The example of finite AP includes 3, 5, 7, 9, 11, 13, 15, 17, 19, 21
• Infinite AP: An AP that does not possess a finite number of terms is called Infinite AP. It does not possess the last Term.
  For example, 2, 4, 6, 8, 10, 12, 14, 16, ....

The Sum of an n Terms

Suppose an arithmetic progression containing "n" terms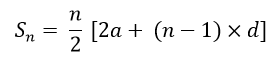

Proof Method

Suppose an arithmetic progression contains "n" terms, and they are in sequence a, a + d, a + 2d, ....., a + (n -1) x d.

Sum of first n terms = a, a + d, a + 2d, ..., a + (n ' 1) d ----------- (1)

Reverse order

S_n=[a+(n-1)×d] + [a+(n-2)×d] + [a+(n-3)×d] +...(a)- - - (ii)

Addition of equations of the above equations

2S_n = [ 2a + (n -1) × d] + [2a + (n -1) x d] + [2a + (n -1) x d] ...... + [ 2a + (n -1) x d ] ( n terms)

2S_n = n x [ 2a + (n ' 1) x d]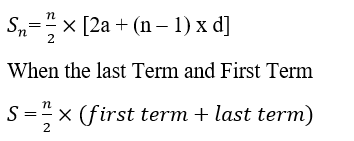

Question: What is the sum of all numbers from 1 to 99?

Ans:1, 2, 3, 4, 5, 6, 7, 9.... , 99

1 = a = First term of the series

1 = d = the common difference

99 = n = the total number of terms

To find the sum, we will use the formula