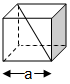
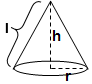
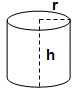
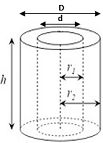
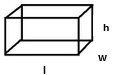
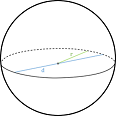
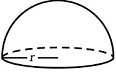
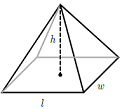
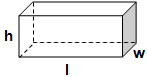
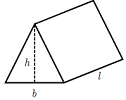
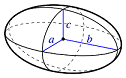
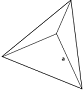
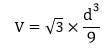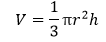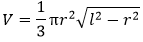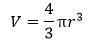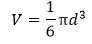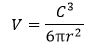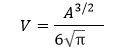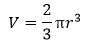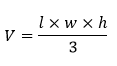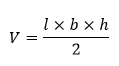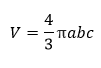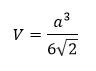Volume Formula

In geometry, three-dimensional shapes are solid objects that have three dimensions. The dimensions contain the length, width, and height of the object. Some examples of 3D shapes are cube, cone, cylinder, pyramid, sphere, etc. We find the volume of these shapes so that we can measure how much space an object takes up to store liquid, gas, etc. There are different volume formulas for different shapes. By using these formulas, we can find the volume of shapes.

In this section, we will learn the volume formula of all the three-dimensional shapes.

Volume

The amount of space occupied by an object is called the volume of that object where an object is a 3D object. We find the volume to measure the capacity of the object or container. We can find the volume of any 3D shape easily by using the formula. If the 3D shape is complicated, we use integral calculus to find the volume.

The volume is denoted by the letter V. We measure the volume in the cubic unit or unit³. In the following table, we have summarized all the volume formulas with the figure for better understanding.

Shape	Figure	Volume Formula	Variables	Constant
Cube		V=a3 When diameter is given:	a: is the length of the side d: is the length of the diameter	-
Cone		When slant height is given:	r: is the radius h: is the perpendicular height l: is the slant height	π: is a constant whose value is 3.14 or 22/7
Cylinder		V=πr2 h	r: is the radius h: is the height	π: is a constant whose value is 3.14 or 22/7
Hollow Cylinder		V=πh(r22-r12)	r1: is the internal radius r2: is the external radius h: is the height of the cylinder D: is the external diameter d: is the internal diameter	π: is a constant whose value is 3.14 or 22/7
Cuboid		V=l×w×h	l: is the length w: is the width h: is the height	-
Sphere		When diameter is given: When circumference is given: When area is given:	r: is the radius d: is the diameter of the sphere C: is the circumference of the sphere A: is the area of the sphere	π: is a constant whose value is 3.14 or 22/7
Hemisphere			r: is the radius	π: is a constant whose value is 3.14 or 22/7
Pyramid			l: is the base length w: is the base width h: is the height of the pyramid	-
Rectangular Prism		V=l×w×h	l: is the length w: is the width h: is the height	-
Triangular Prism			l: is the length w: is the width h: is the height	-
Ellipsoid			a, b, and c: are semi-axes of ellipsoid	π: is a constant whose value is 3.14 or 22/7
Tetrahedron			a: is edge of tetrahedron	-