Simplify FractionsSimplifying or reducing fractions means to convert the fraction into simplest form. A fraction is called the simplified fraction if 1 is the only common factor of its numerator and the denominator. To simplify a fraction, choose the highest number that can completely divide both the numerator and the denominator. How to Simplify FractionThere are three methods to simplify a fraction:
Using Repeated DivisionIn this method, we choose a small number (such as 2, 3, 4, 5) to divide a fraction. The selection of a number is decided by the fraction by looking at the fraction. Suppose, a fraction is To simplify the fraction, follow the steps given below:
Example 1: Reduce the fraction Solution: In the fraction 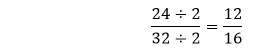
We get the fraction 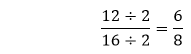
We get the fraction 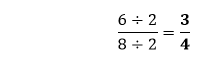
The fraction Hence, the simplified fraction is Example 2: Simplify the fraction Solution: In the fraction 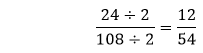
We get the fraction 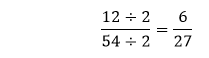
We get the fraction 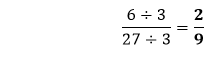
The fraction Hence, the simplified fraction is Example 3: Simplify the fraction Solution: In the fraction 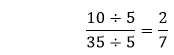
The fraction Hence, the simplified fraction is Using Greatest Common Factor (GCF)The greatest common factor is the number that divides the number completely. While reducing the fraction, it is easy to repeatedly divide the numerator and the denominator by the greatest common factor. If the GCF of the numerator and denominator is 1, the fraction cannot be reduced further. It means the fraction is in its simplest form. To simply the fraction, follow the steps given below.
Note: Every number is divisible by 1 and itself. So, 1 and the number itself are the two factors for each number.Let's see some examples. Example 4: Simplify the fraction Solution: Step 1: Factors of the numerator (12): 1, 2, 3, 4, 6, 12 Factors of the denominator (18): 1, 2, 3, 6, 9, 18 Step 2: Common Factors: 1, 2, 3, 6 Step 3: Greatest Common Factor: 6 Step 4: We will divide both the numerator and the denominator by the greatest common factor, i.e., 6. 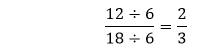
We cannot further simplify the fraction because both the numerator and the denominator are divisible by itself and having GCF 1. Step 5: Hence, the simplified fraction is Example 5: Reduce the fraction Solution: Step 1: Factors of the numerator (25): 1, 5, 25 Factors of the denominator (75): 1, 3, 5, 15, 25, 75 Step 2: Common Factors: 1, 5, 25 Step 3: Greatest Common Factor: 25 Step 4: We will divide both the numerator and the denominator by the greatest common factor, i.e., 25. 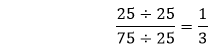
We cannot further simplify the fraction because both the numerator and the denominator are divisible by itself and having GCF 1. Step 5: Hence, the simplified fraction is Example 6: Reduce the fraction Solution: Step 1: Factors of the numerator (8): 1, 2, 4, 8 Factors of the denominator (10): 1, 2, 5, 10 Step 2: Common Factors: 1, 2 Step 3: Greatest Common Factor: 2 Step 4: We will divide both the numerator and the denominator by the greatest common factor, i.e., 2. 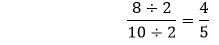
We cannot further simplify the fraction because both the numerator and the denominator are divisible by itself and having GCF 1. Step 5: Hence, the simplified fraction is Example 7: Simplify the fraction Solution: Step 1: Factors of the numerator (30): 1, 2, 3, 5, 6, 10, 15, 30 Factors of the denominator (36): 1, 2, 3, 4, 6, 9, 12, 18, 36 Step 2: Common Factors: 1, 2, 3, 6 Step 3: Greatest Common Factor: 6 Step 4: We will divide both the numerator and the denominator by the greatest common factor, i.e., 6. 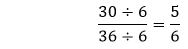
We cannot further simplify the fraction because both the numerator and the denominator are divisible by itself and having GCF 1. Step 5: Hence, the simplified fraction is Using Prime Factor TreeIn this method, we find the prime factors of the numerator and the denominator and cancel out the common factors. Prime Factor: Prime factor is the prime number that is divisible by itself. For example, 2, 3, 5, 7, 11, etc. To find the prime factor, branch off the given number into two numbers in which one must be prime. Repeat it until we do not get both numbers as prime. To simplify the fraction using the prime factor tree, follow the steps given below.
Let's understand it through examples. Example 8: Reduce the fraction Solution: Let's find the prime factors of 24 and 60. 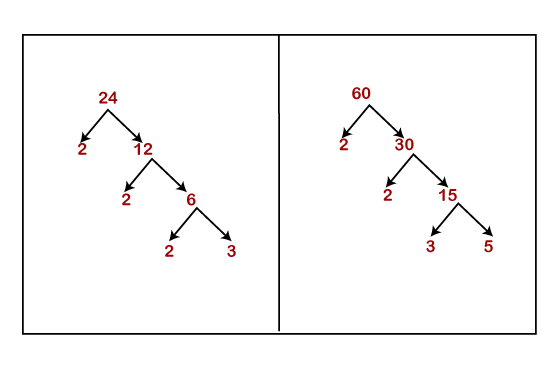
Write the prime factors with the multiplication sign. 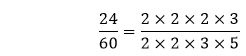
Cancel out the common factors, we get: 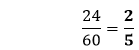
Hence, the simplified fraction is Example 9: Simplify the fraction Solution: Let's find the prime factors of 820 and 240. 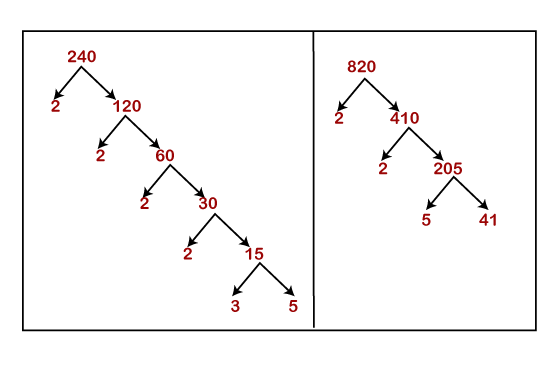
Write the prime factors with the multiplication sign. 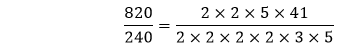
Cancel out the common factors, we get: 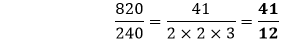
Hence, the simplified fraction is
Next TopicPythagoras
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share




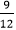 given, and we have chosen the number 5 to divide the fraction. It would be a wrong selection of the number because it would not go into either number. Instead of 5, if we choose 3, it would be a suitable number to use. Hence, the selection of the number must be appropriate.
given, and we have chosen the number 5 to divide the fraction. It would be a wrong selection of the number because it would not go into either number. Instead of 5, if we choose 3, it would be a suitable number to use. Hence, the selection of the number must be appropriate.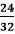 .
.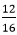 that is still divisible by 2. So, we will divide it again by 2.
that is still divisible by 2. So, we will divide it again by 2.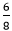 that is still divisible by 2. So, we will divide it again by 2.
that is still divisible by 2. So, we will divide it again by 2.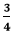 cannot be further simplified because 3 is a prime number and divisible by 1 and itself. The denominator is not divisible by 3.
cannot be further simplified because 3 is a prime number and divisible by 1 and itself. The denominator is not divisible by 3.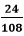 .
.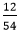 that is still divisible by 2. So, we will divide it again by 2.
that is still divisible by 2. So, we will divide it again by 2.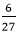 in which the numerator is divisible by 2, but the denominator is not. So, we will pick such a different number that can divide both the numerator and the denominator. Hence, we will divide the fraction
in which the numerator is divisible by 2, but the denominator is not. So, we will pick such a different number that can divide both the numerator and the denominator. Hence, we will divide the fraction 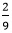 cannot be further simplified because 2 is a prime number and divisible by 1 and itself. The denominator is not divisible by 2.
cannot be further simplified because 2 is a prime number and divisible by 1 and itself. The denominator is not divisible by 2.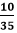 .
.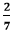 cannot be further simplified because 2 is a prime number and divisible by 1 and itself. The denominator is not divisible by 2.
cannot be further simplified because 2 is a prime number and divisible by 1 and itself. The denominator is not divisible by 2.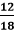 .
.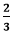 .
.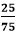 .
.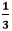 .
.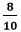 .
.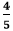 .
.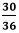 .
.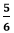 .
.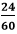
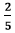 .
.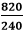 .
.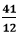 .
.




