Cube 1 To 50

Cubes, a captivating mathematical concept, have intrigued human minds for centuries. In this article, we embark on a journey through the numbers 1 to 50, uncovering the secrets and patterns hidden within their cubes. From simple calculations to profound mathematical relationships, we delve into the world of cubes and shed light on their significance. So, let's begin our exploration of cube numbers from 1 to 50!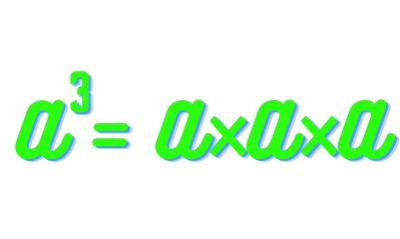

Understanding Cube Numbers

Cube numbers are the result of multiplying an integer by itself twice. For instance, the cube of 2 is 2 × 2 × 2, which equals 8. The first few cube numbers are 1, 8, 27, and 64. Each subsequent cube is obtained by multiplying the next integer by itself twice. Visualizing these numbers as three-dimensional cubes, we can observe their geometric interpretation.

Patterns and Observations

The most striking pattern among cube numbers is the relationship they share. Each cube number is equal to the previous number plus the current odd number. For example, 8 (2³) can be obtained by adding 7 (2 × 3 - 1) to 1 (the previous cube number). This pattern holds true for all cube numbers. Additionally, cube numbers have a unique relationship with square numbers. The difference between consecutive cubes is always a consecutive sequence of square numbers. For instance, the difference between 8 and 1 is 7, which is a square number (3^2). This relationship between cubes and squares provides an intriguing connection in number theory.

Cube numbers also exhibit parity patterns. If an integer is odd, its cube will also be odd, and if an integer is even, its cube will be even. This characteristic is a consequence of the multiplication rules governing even and odd numbers.

Furthermore, exploring the sums of consecutive cubes reveals an interesting relationship to square numbers. The sum of the first n cubes is always equal to the square of the sum of the first n integers. For example, the sum of the first three cubes (1 + 8 + 27) is 36, which is the square of the sum of the first three integers (1 + 2 + 3 = 6).

Properties of Specific Cube Numbers

Within the series of cube numbers from 1 to 50, there are several noteworthy properties. Some numbers, like 8, 27, and 64, are perfect cubes-numbers that can be expressed as the cube of an integer. On the other hand, prime cube numbers, such as 2 and 3, do not have any factors other than 1 and themselves. Composite cube numbers, like 27 and 48, have factors other than 1 and themselves.

Cube roots are an essential concept related to cube numbers. The cube root of a number is the value that, when multiplied by itself twice, results in the original number. Cube roots are particularly useful in solving cubic equations, which have wide-ranging applications in various fields of science and engineering.

Real-World Applications

Cubes find practical applications in geometry, where they serve as the building blocks for three-dimensional shapes. From cubes, we can form other polyhedra and analyze their properties. Architects and engineers utilize cubes in construction and design, as they provide stability and symmetry in various structures. Furthermore, cryptography, the science of secure communication, employs cubes in encryption algorithms, ensuring the confidentiality and integrity of data transmission.

Cubes of Numbers 1 to 50

Conclusion

From their geometric interpretation to the intricate patterns they exhibit, cube numbers from 1 to 50 offer a captivating journey through the world of mathematics. Understanding the cube number pattern, exploring their relationships to square numbers, and observing their parity properties provide valuable insights into the nature of numbers.