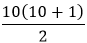Natural NumbersDefinitionThe natural numbers are the numbers that we use in counting objects or things. In other words, natural numbers are the set of all the whole numbers, excluding zero. It is a part of the real number. It includes only positive integers. Remember that 0, fractions, decimals, and negative numbers are not the natural number. The natural numbers start from 1 and go up to infinity. For example, 1, 2, 3, 4, 5, 6, and so on. The natural numbers contain all the whole numbers, excluding zero. It means all the natural numbers are whole numbers, but all whole numbers are not natural numbers because whole numbers also include 0. 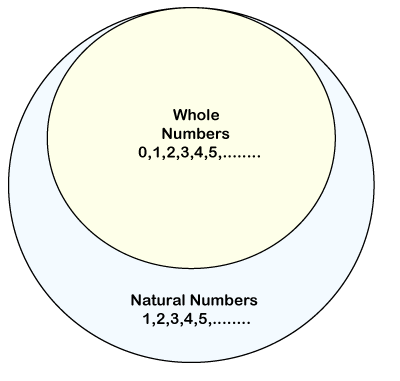
First 50 natural numbers are: 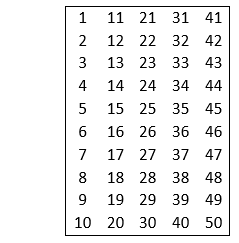
Notation of Natural NumbersThe set of natural numbers is denoted by the letter N. Set of Natural NumbersThe set of natural numbers is an infinite set. We can represent the set of natural numbers in the following three forms:
Facts About Natural Numbers
Properties of Natural NumbersThere are four main properties of natural numbers:
Closure PropertyThe natural numbers follow the closure property under addition and multiplication operation. It means that when we apply addition or multiplication on two or more natural numbers, we always get a natural number as the result. Suppose, a, b are two natural numbers, and c is the result, then:
a+b=c (natural number)
a×b=c (natural number) For example, 9+5=14,12+3=15, etc. the sum 14 and 15 are also natural numbers. Similarly, in multiplication 20×3=60,15×5=75, etc. product 60 and 75 are also natural numbers. In the case of subtraction and division, the natural numbers may or may not follow the closure property. It means that when we apply subtraction or division on two or more natural numbers, it may yield negative results and decimal quotient, respectively. Suppose, a, b are two natural numbers, and c is the result, then:
a-b=c (natural number) ifa>b
a÷b=c (natural number) if a is completely divisible by b For example, 9-5=4,12-3=9, etc. the resultant 4 and 9 are also natural numbers. But when we subtract 5-9=-4, it does not yield a natural number. Similarly, in division 20÷5=4,15÷5=3, etc. the quotient 5 and 3 are also natural numbers. But when we divide 3÷2=1.5, it does not yield a natural number.
a-b=-c (not a natural number) ifa<b
a÷b=c,(not a natural number) if a is not completely divisible by b Commutative PropertyThe addition and multiplication operation of natural numbers follow the commutative property. Suppose, a and b are two natural numbers, then:
a+b=b+a
a×b=b×a The subtraction and division of natural numbers do not follow the commutative property.
a-b≠b-a
a÷b≠b÷a Associative PropertyThe addition and multiplication operation of natural numbers follow the associative property.
a+(b+c)=(a+b)+c
a×(b×c)=(a×b)×c The subtraction and division operation of natural numbers do not follow the associative property.
a-(b-c)≠(a-b)-c
a÷(b÷c)≠(a÷b)÷c Distributive PropertyThe multiplication of natural numbers is always distributive over addition and subtraction.
a×(b+c)=ab+ac
a×(b-c)=ab-ac Existence of IdentityIf we add 0 to a natural number or multiply a natural number by 1, we get the same natural number. Suppose, a is a natural number, then:
a+0=a
a×1=a Let's see some examples. Example 1: From the following list of numbers, pick the natural numbers and non-natural numbers.
-4,20,
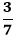 ,2.67,6,90,100000 ,2.67,6,90,100000
Solution: Natural Numbers: 20,6,90,100000 Non-natural Numbers: -4, Example 2: Write the first 10 natural numbers. Solution: First 10 natural numbers are: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Example 3: Write the natural numbers between 20 and 30. Solution: Natural Numbers between 20 and 30 are: 21,22,23,24,25,26,27,28,29,30 Example 4: What is the sum of the first 10 natural numbers. Solution: First 10 natural numbers are: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 There are two ways to find the sum of natural numbers:
Using the Addition of Operation 1+2+3+4+5+6+7+8+9+10=55 It is a time-consuming process if we have a large number of natural numbers to add. So, we do not use it usually. Using the Formula 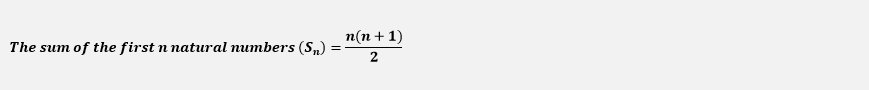
We have to find the sum of the first 10 natural numbers, so n = 10. Putting the value of n in the above formula, we get: The sum of the first 10 natural numbers (S10)= 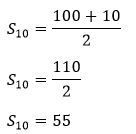
Hence, the sum of the first 10 natural numbers is 55. Example 5: Find the sum of the first 45 natural numbers. Solution: We have to find the sum of the first 45 natural numbers. So, n = 45. Putting the value of n in the above formula, we get: 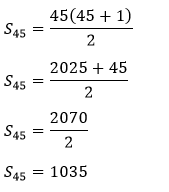
Hence, the sum of the first 45 natural numbers is 1035.
Next TopicBar Graph
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share