Perimeter of Rectangle

In mathematics, the area and the perimeter are the two most important terms that we deal with. It can be applied to different shapes, regular or irregular.

The word perimeter is the combination of two Greek words, peri and metron. The word peri means around, and metron means to measure. Hence, the word perimeter means the total length of a 2D shape. In this section, we will learn how to find the perimeter of the rectangle.

Perimeter

In mathematics, the word perimeter means a path that surrounds an area. In other words, it is the boundary of a two-dimensional shape. It refers to the total length of the sides or edge of a polygon (a two-dimensional figure with angles). For example, the wooden fence around the garden. The unit of the perimeter is centimeter (cm), meter (m), feet (ft), etc.

Suppose, we want to cover the field with iron wire from the protection of animals, how will we know what length should be the iron wire.

Formula of the Perimeter of Rectangle

A rectangle is a four-sided shape. Its two sides are equal and parallel to each other. All the angles are 90°. We know that, the perimeter is the total boundary of the two-dimensional shape and a rectangle has four sides.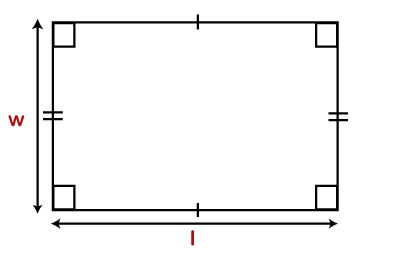

Therefore,

P=l+w+l+w
P=2l+2w

Where:

: is the length of the rectangle.

w: is the width of the rectangle.

Remember that the area and the perimeter are two different things. Area means the space (inside) covered by shape or an object. While the perimeter is the distance (outside) around an object or shape. It means a figure or an object having the same perimeter can have a different area. An object having the same area can have a different perimeter.

Let’s see some examples based on the above formula.

Example 1: Find the perimeter of the following figure.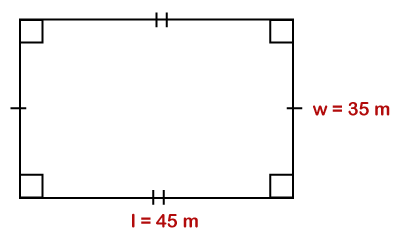

Solution:

Given, l=45 m and w=35 m

According to the formula:

P=2(45+35)
P=2(80)
P=160 m

Hence, the perimeter of the given figure is 160 m.

Example 2: The length and the width of a rectangle are 50 and 30 feet, respectively. Find the perimeter.

Solution:

Given, l=50 ft and w=20 ft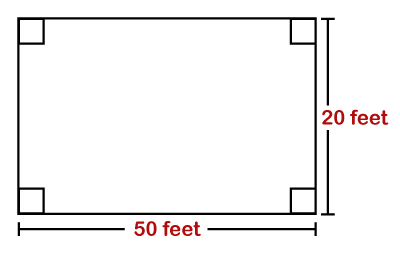

According to the formula:

P=2(50+20)
P=2(70)
P=140 m

Hence, the perimeter of the given figure is 140 m.

Example 3: The perimeter of a field is 190 cm. If the width is 40 cm. Calculate the length of the rectangle.

Solution:

Given, P=190 cm,and w=40 cm

length (l)=?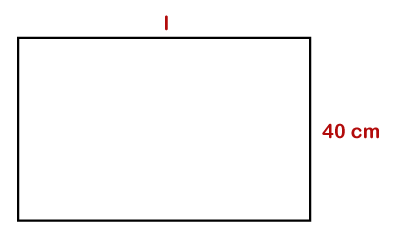

According to the formula:

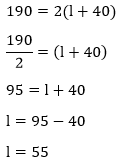
Hence, the length of the rectangle is 55 cm.

Example 4: One side of a rectangle is 17 cm and another side is 12 cm. What is the perimeter of the rectangle?

Solution:

Given, l=17 cm and w=12 cm

According to the formula:

P=2(17+12)
P=2(29)
P=58 m

Hence, the perimeter of the rectangle is 58 cm.

Example 5: What is the perimeter of the following rectangle.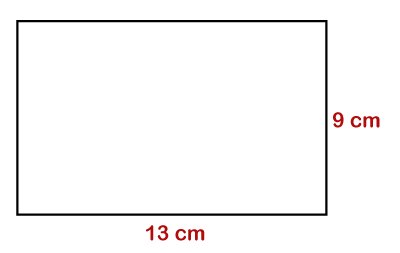

Solution:

Given, l=13 cm and w=9 cm

According to the formula:

P=13+9+13+9
P=44 cm

Hence, the perimeter of the rectangle is 44 cm.