Stewart's Theorem

Geometry is the branch of Mathematics that studies shapes and their different properties, and it has been a basic field of study for a long time. In this concept, a special shape, "Triangle," has a special place in this geometry concept, as they are the simplest polygon with three sides, which is the minimum number of sides to make a polygon. Triangles are important to understanding more complex geometric shapes and play an important role in various mathematical and scientific concepts. There are so many theorems to calculate or show the properties of triangles in different manners, and one of the most complex and important theorems is Stewart's Theorem; it is related to the relationship among sides of a triangle and a cevian: it is a line that joins one vertex of the triangle to the opposite side of that triangle. So, in this article, we will learn about the concept of Stewart's Theorem, its history, and applications, and end this article with a conclusion.

History

This Theorem is named after the Scottish Mathematician "Matthew Stewart," this Stewart theorem came into existence in the early 18^th century; he was a prominent mathematician at that time who lived from 1717 to 1785, and he also contributed to various fields of study that include mathematics. His work was marked by an approach that combines elements of philosophy, physics and, of course, mathematics.

The result of Stewart's hard work in mathematics was Stewart's Theorem, which was first published in his book, "Some General Theorems of Considerable Use in the Higher Parts of Mathematics" in 1746; this Theorem shows the relationship Stewart had been working on, between the sides of the triangle and a cevian lines.

Stewart's Theorem emerged from his exploration of geometric relationships within triangles; in particular, Stewart was to show the relationships between the sides of the triangle and the line segment joining one vertex to a point on the opposite side. This line segment, known as a cevian, made Stewart curious, and he tried to uncover a mathematical relationship that would allow for the determination of unknown quantities in a triangle when some things were known.

Understanding Stewart's Theorem

Before we get to understand the concept of the Theorem itself, it is important to understand some basic concepts and definitions that are related to triangles and cevians.

1. Triangles

A triangle is a polygon with three sides, three vertices, and three angles; triangles are categorised based on the relationships between their sides and angles. Some common types of triangles are equilateral triangles (all sides and angles are equal), isosceles triangles (two sides and two angles are equal), and scalene triangles (all sides and angles are different).

2. Cevians

A cevian is a line segment that joins one vertex of a triangle to a point on the opposite side; there are various types of cevians in a triangle, which include medians, altitudes, and angle bisectors. Each type serves a different concept and has distinct geometric properties.

Statement of Stewart's Theorem

Stewart's Theorem can be stated as follows:

In a triangle ABC, let 'a' be the length of side BC, 'b' be the length of side AC, and 'c' be the length of side AB, and let 'd' be the length of the cevian AD, where D is any point on side BC. Then, according to Stewart's Theorem, the following relationship:

b² * m + c² * n = a * d² + m * n * a

b² * m + c² * n = a * (d² + m * n)

Where:

• m is the length of BD (the segment from B to D).
• n is the length of the CD (the segment from C to D).

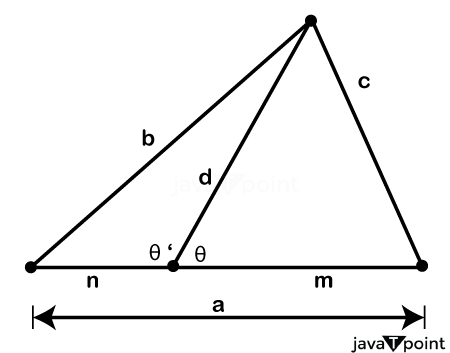
In other words, this Theorem relates the lengths of the cevian segments (m and n) and the length of the sides of the triangle (a, b, and c). The Theorem is particularly useful when you need to find the length of one cevian segment (for example, AD) while knowing the lengths of the other two cevian segments (BD and CD) and the sides of the triangle (a, b, and c).

Proof of Stewart's Theorem

There are several ways to prove Stewart's Theorem, but we will use the Law of Cosines and the basic properties of triangles.

Consider triangle ABC; using the Law of Cosines, we can express the cosine of angle ? in terms of the sides of the triangle:

Cos (?) = (m² + d² - c²) / (2dm) … (1)

Similarly, using the Law of Cosines, we can express the cosine of angle ?' in terms of the sides of the triangle:

Cos (?') = (n² + d² - b²) / (2dn) … (2)

As we can see from the image that, ? + ?' = 180?.

• ? = 180 - ?'
• Cos (?) = Cos (180 - ?')
• Cos (?) = - Cos (?') … (3)

So, putting equation (1) and (2) in equation (3), we get:

• (m² + d² - c²) / (2dm) = (n² + d² - b²) / (2dn)
• n * (m² + d² - c²) = m * (n² + d² - b²)
• nm² + nd² - nc² = mn² + md² - mb²

After arranging and some calculations, we get

• b² * m + c² * n = a * d² + m * n * a
• b² * m + c² * n = a * (d² + m * n), Which is the required result.

Some Geometric Explanation

To get a deeper understanding of Stewart's Theorem, let's explore its geometric explanation; it specifically provides a way to balance the draw of the cevian AD on the sides of the triangle. On the left side of the equation, we have the squares of the lengths of AC and AB, i.e., b2 and c2, multiplied by the lengths of the cevian segments BD and CD, i.e., m and n. These terms represent the "opposite sides" of the triangle with respect to cevian AD; on the right side of the equation, we have the square of the length of the side BC (a²) multiplied by the length of the cevian AD (d²) and the product of the cevian segments BD and CD (m * n). These terms represent the "opposite side" of the triangle with respect to the side AD.

In short, Stewart's Theorem shows an equation balancing the cevian AD and the sides of the triangle ABC, highlighting the connections between these geometric elements.

Applications of Stewart's Theorem

Stewart's Theorem has a wide range of applications in various fields, including mathematics, physics, engineering, and even computer graphics; let's discuss some practical applications where Stewart's Theorem applies:

1. Trigonometric Calculations: One of the most common applications of Stewart's Theorem is trigonometric calculation; by rearranging the Theorem's equation, you can get trigonometric relationships that involve the sides and angles of the triangle. This can be particularly useful in solving complex trigonometric equations and proving trigonometric identities.
2. Calculating Lengths of Cevian Segments: Stewart's Theorem is mostly used to determine the length of a cevian segment within a triangle when other relevant lengths are given; this is very useful in geometry problems and real-world applications where triangles are involved, such as architecture and surveying.
3. Analysing Mechanical Systems: In physics and engineering, Stewart's Theorem can be used to analyse mechanical systems and calculate forces and distances; in short, it is particularly useful in cases that involve structural elements and others where forces are distributed across multiple components.
4. Computer Graphics: In computer graphics and animation, Stewart's Theorem can be applied to calculate the positions and movements of objects within a 3-D space, and it plays a role in creating realistic animations by simulating the motion of objects and characters.
5. Solving Geometry Problem: Stewart's Theorem usually appears in geometry competitions and problem-solving exercises, and it offers a powerful and useful tool for solving complex geometric puzzles, giving a systematic way to find the solutions.

Conclusion

Stewart's Theorem was discovered out of the curiosity and explorations of Matthew Stewart in mathematics; this Theorem has proven to be a very important concept in the world of geometry and mathematics as a whole. It is simplicity and brief expression provide a powerful tool for understanding and solving complex problems involving triangles and cevians; far from mathematics, the Theorem's applications lie in physics, engineering, computer graphics, and various other fields.

As we continue to explore the complexness of geometry and its applications in the modern world, Stewart's Theorem serves as a reminder of the importance and usefulness of mathematical discoveries; it invites mathematicians, scientists, and problem solvers of all kinds to show the mysteries of triangles and discover new connections and relationships in the world of mathematics.