Volume of a ConeIn this section, we will learn what is the cone, types of cone, the formula of volume of a cone, its derivation. Along with this, we will also learn how to find the volume of a cone. ConeThe cone is a three-dimensional geometrical shape that has a circular base (surface) and a vertex. The vertex is connected with the base through the two slanted line segments. These two-line segments connected at a common point called the vertex. Ice-cream cone and birthday cap is the best example of the cone. The following figure shows the shape of a cone. 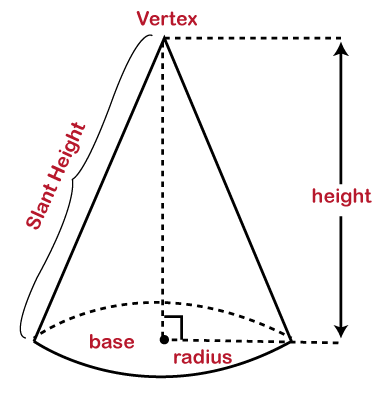
Types of ConeThere are two types of cones:
Right Cone or Cone: It is a cone whose vertex is vertically above the center of the base. The following figure shows the shape of the right cone. 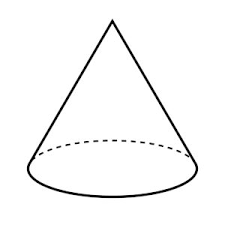
Oblique Cone: The cone whose pointed part is not vertically above the center of the base is called an oblique cone. The following figure shows the shape of an oblique cone. 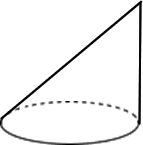
The volume of a ConeIn mathematics, the area enclosed by an object is called the volume of that object. The cone is also a three-dimensional geometrical shape, so the area covered by a cone is called the volume of a cone. It is denoted by the letter V. Note: The radius and height must be in the same unit. Convert the units before calculation if they are different.Unit of the VolumeThe unit of the volume is a cubic unit or unit3. The Formula of the Volume of a ConeThe volume (V) of a cone with radius (r) is one-third the area of the base time height. In other words, the volume of a cone is one-third of the volume of a cylinder. We can easily find out the volume of a cone by using the following formula if the radius and height are known. 
Note: The above formula is also used to find the volume of an oblique cone.The volume of the cylinder will be three times the volume of the cone if the height of the cylinder and cone are equal. The volume of a cone when slant height (l) is given: 
Derivation of the FormulaIn the following figure, we have a cylindrical shape and a conical shape of the same height and radius. Put the conical shape is inside the cylindrical shape. Now pour the water in the cylindrical shape. We see that it does not fill the cylinder up to the capacity. After repeating this process two to three times, we see that the same experiment fills the cylindrical shape up to the capacity. Therefore, the volume of a cone is equal to the one-third volume of a cylinder. 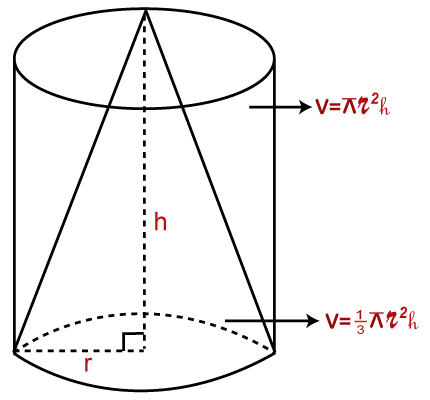
Consider the above figure, the radius of the circular base is r, and the height is h. We know that the volume of a cylinder is the product of the area of the base and its height. The Volume of a Cylinder (V)=Area of the base×height of cylinder V=πr2 h We know that the volume of a cone is equal to the one-third volume of a cylinder. Hence, The Volume of a Cone (V)= 
Where: V: is the volume of the cone. π: is a constant whose value is 22/7 or 3.14. r: is the radius of the base. h: is the perpendicular height of the cone. Let's see how to find the volume of a cone. Example 1: The perpendicular height of a cone is 15 cm, and the radius is 4 cm. Find the volume of the cone. (Pi = 3.14) 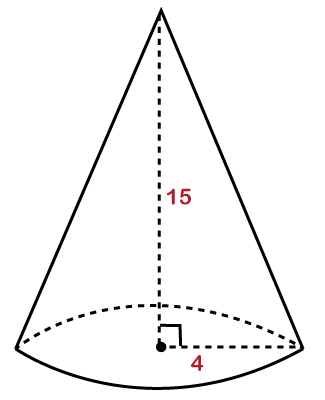
Solution: Given, height (h)= 15 cm radius (r) = 4 cm We know the formula of volume of a cone: 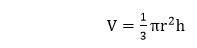
Putting the values in the above formula, we get: 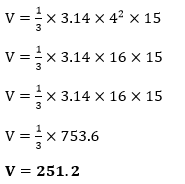
Hence, the volume of the cone is 251.2 cm3. Example 2: The diameter of a cone is 10 meters, and its height is 19 meters. Find the volume and also represent it graphically. 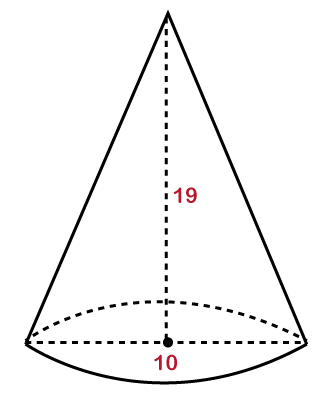
Solution: Given, height (h)= 19 m diameter = 10 m We know that the radius is half the diameter. Hence, 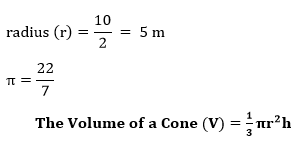
Putting the values in the above formula, we get: 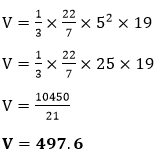
Hence, the volume of the cone is 497.6 m3. Example 3: The slant height of a birthday cap is 30 cm, and the radius of the base is 12 cm. Find the volume. 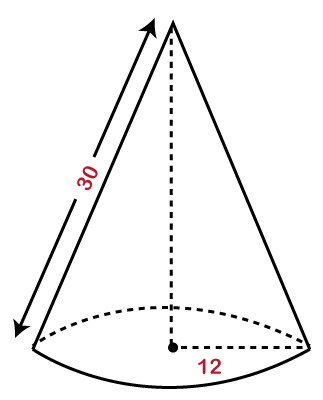
Solution: Given, slant height (l) = 30 cm radius (r) = 12 cm π=3.14 We know the formula of volume when slant height and radius are given. 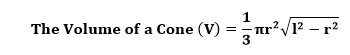
Putting the values in the above formula, we get: 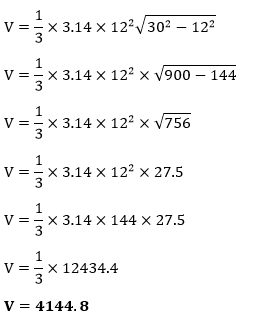
Hence, the volume of the cone is 4144.8 cm3. Example 4: The volume of a pipe is 223 m3. Find the volume of the cone. Solution: Given, the volume of a cylinder (V) = 223 m3 The volume of a cone (V) =? We know that the volume of the cone is one-third of the volume of the cylinder. Therefore: V= V=74.33 Hence, the volume of the cone is 74.33 m3. Example 5: If the height of a cone and a cylinder is 12 cm and the radius is 4 cm, prove that the volume of the cylinder will be three times the volume of the cone. Solution: Given, height (h) = 12 cm radius (r) = 4 cm 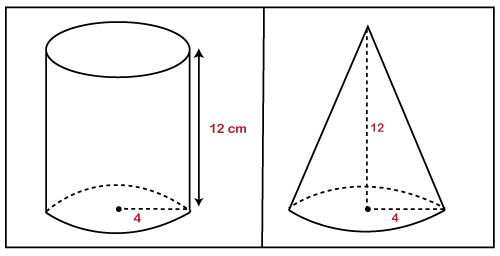
We know that, The Volume of a Cylinder (V)=πr2 h Putting the values in the above formula, we get: V=3.14×42×12 We also know that, The Volume of a Cone (V)= Putting the value in the above formula, we get: The Volume of a Cone (V)= The Volume of a Cone (V)=200.96 To verify the answer, multiply the volume of the cone by 3, we get the volume of the cylinder. Hence, 200.96×3=602.88 Hence proved.
Next TopicVolume of a Cube
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share




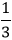 ×Volume of Cylinder
×Volume of Cylinder




