Frequency Formula

Waves are all around us, from the gentle ripples of a pond to the powerful vibrations of sound and light. The study of waves is essential in various scientific fields such as physics, engineering, and telecommunications. A fundamental concept in wave analysis is frequency, a key parameter that determines wave behavior and properties. In this article, we look at the formula for frequency and consider its importance in the world of waves.

What is Frequency

Frequency is defined as the number of wave cycles or oscillations per unit of time, often denoted by the symbol 'f'. It measures the number of times a wave repeats its pattern and is usually expressed in units of hertz (Hz), which equals cycles per second. The higher the wave frequency, the more cycles it passes through in a given period of time.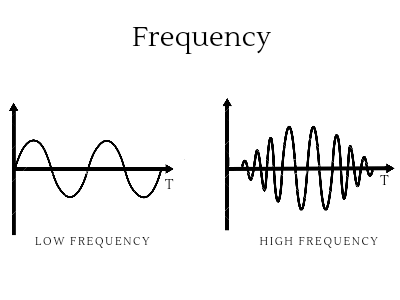

Frequency Formula

The frequency formula provides a mathematical relationship between the frequency of a wave, the velocity of the wave, and the wavelength. The wavelength (symbolized by the Greek letter λ, lambda) is the spatial distance between two consecutive points in a wave that is in phase, meaning they have the same position within their respective cycles.

The frequency formula can be expressed as: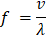

In this formula, 'f' represents the frequency, 'v' denotes the velocity of the wave, and 'λ' signifies the wavelength.

Components of Frequency Formula

Let's take a closer look at each of these components and understand how they contribute to the overall behavior of waves.

• Frequency (f): As mentioned earlier, frequency measures the number of cycles completed by a wave in a given time period. It determines the pitch of a sound wave and the color of light. Higher-frequency waves are perceived as higher-pitched sounds and are associated with shorter wavelengths.
• Velocity (v): The velocity of a wave refers to the speed at which it propagates through a medium. Different types of waves, such as sound waves, light waves, and water waves, have varying velocities depending on the properties of the medium they travel through. For example, sound waves travel at different velocities in air, water, and solids.
• Wavelength (λ): Wavelength is the distance between two consecutive points in a wave that is in phase. It is inversely related to frequency, meaning that as the frequency of a wave increases, its wavelength decreases. This relationship is represented by the formula λ = v / f derived from the frequency formula.

Example Using Frequency Formula

Question:

Suppose a sound wave travels through air with a velocity of 343 meters per second (m/s). If the wavelength of the wave is 1 meter (m), we can use the frequency formula to calculate the frequency of the wave:

Solution:

f = v / λ

f = 343 m/s / 1 m

f = 343 Hz

Therefore, the sound wave frequency in this example is 343 Hz.

Uses of Frequency Formula

The frequency formula is a powerful tool for analyzing waves across various disciplines. It allows scientists and engineers to understand and manipulate the properties of waves, enabling advancements in fields like telecommunications, acoustics, and optics.

• Telecommunication: One area where the frequency formula finds extensive applications is in telecommunications. The transmission of information through signals, such as radio waves or electromagnetic waves, relies on understanding and manipulating frequencies.
• Acoustic: In the field of acoustics, the frequency formula helps us understand the characteristics of sound waves. By analyzing the frequency content of a sound, we can identify its pitch and timbre. Musical instruments, for instance, produce different tones based on the frequencies at which they vibrate.
• Optics: In optics, the frequency of light waves determines their color. The frequency formula helps us understand how different frequencies of light interact with matter. For example, in spectroscopy, scientists use the frequency formula to analyze the interaction between light and atoms or molecules, providing valuable information about their composition and structure.

Conclusion

The frequency formula, expressed as f = v / λ, plays a vital role in our understanding of waves. By relating frequency, velocity, and wavelength, it allows us to quantify and manipulate various wave phenomena. The formula finds widespread applications in fields such as telecommunications, acoustics, optics, and beyond, enabling advancements in technology and scientific research. By mastering the frequency formula, we unlock the secrets of waves and open doors to new possibilities in multiple domains.