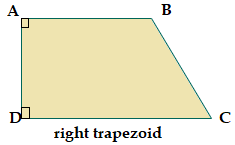
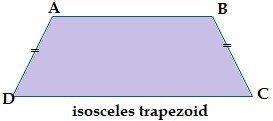
Trapezoid Parallel Sides

A trapezoid is a flat four-sided 2D closed shape with a pair of parallel sides (opposite sides). It is also sometimes called trapezium (UK). The parallel side of a trapezoid are called the bases, and the non-parallel sides are legs. It may have parallel legs. When the parallel sides make the two equal angles or when the two non-parallel sides are equal, it is called isosceles trapezoid.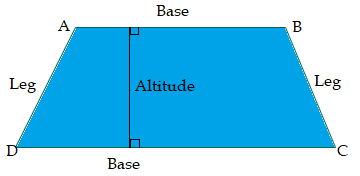

The parallel sides of the trapezoid can be vertical, horizontal, and slanting. The perpendicular distance between two parallel sides is called its altitude.

Properties of Trapezoid

• A trapezoid's two opposite sides (one pair) are parallel.
• Its two diagonals intersect each other.
• A line connecting non-parallel sides at mid-points is always parallel to the bases and half of the sum of parallel sides.
• The angles formed on the same side of a leg are called adjacent angles, and these angles are supplementary.
• If all the opposite sides are parallel in trapezoid is called a parallelogram.
• If all the opposite sides are parallel, all its sides are equal in length and form a right angle at each point called a square.
• If all the opposite sides are parallel, their opposite sides are only equal in length and form a right angle at each point called a rectangle.

Types of Trapezoid

The trapezoid is categorized into three different types. These are the following:

1. Right trapezoid: when its two angles are right angles, called a right trapezoid.
   
2. Isosceles trapezoid: When its two non-parallel sides are equal in length called isosceles trapezoid.
   
3. Scalene trapezoid: when none of its sides are equal in length or not any equal angles called scalene trapezoid.
   

Area of Trapezoid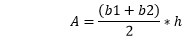

Where A is an area, b1 and b2 are the lengths of two parallel sides, and h is a perpendicular height of the trapezoid.

For example:

Look at the below figure of a trapezoid with the unit of length 3, 10, 11, 8, which has 7 units of perpendicular height.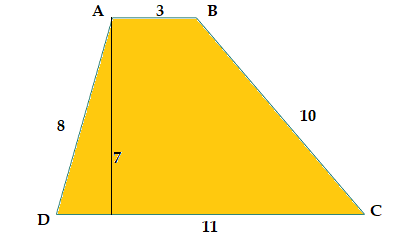

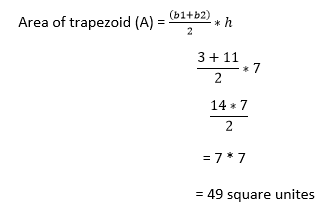
Area of Isosceles Trapezoid

Suppose that b1 and b2 are the lengths of parallel sides of trapezoid ABCD, such as b1 and b2 are the length of the opposite parallel to base b1.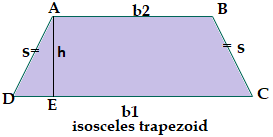

Where, b1 > b2

Now, s is the length of each non-parallel side, and h is the height of an isosceles trapezoid. Where:

CD = b1, AB = b2, and AD = BC = s

When we draw a perpendicular line (h) from AB to meet CD at E, it makes a right angle at AED and AEC.

Then the perpendicular height (h) is: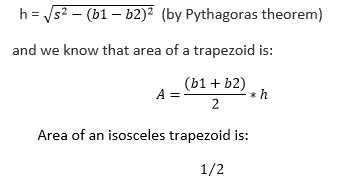

Perimeter of a trapezoid (trapezium)

The addition of all four sides of a trapezoid is known as the perimeter of a trapezoid. The formula to calculate the perimeter of a trapezoid is given below:

Perimeter of trapezoid (P) = a + b + c + d units

Where a, b, c, d are the sides of the trapezoid.

For example:

Calculate the perimeter of the below-given trapezoid: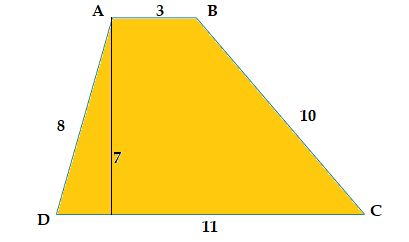

P = a + b + c + d

= 3 + 10 + 11 + 8

= 32 unit

Perimeter of isosceles Trapezoid

If b1 and b2 are the lengths of corresponding parallel sides and s is the length of each non-parallel sides of an isosceles trapezoid, then its perimeter will be: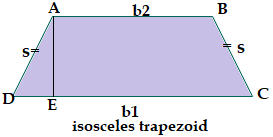

Perimeter (P) = b1 + b2 + 2s

For example: assume that the length of parallel sides of isosceles trapezoid is 12 and 10 units and the length of non-parallel sides is 5 units each. Then calculate its perimeter:

Given, b1 = 12, b2 = 10, and s = 5

Perimeter of isosceles trapezoid (P) = b1+ b2 + 2s

= 12 + 10 + 2(5)

= 12 + 10 + 10

= 32 unit

Median of a Trapezoid

A median is a line that connects non-parallel sides at mid-points is always parallel to the bases and half of the sum of parallel sides. It is also called as midline or midsegment of a trapezoid.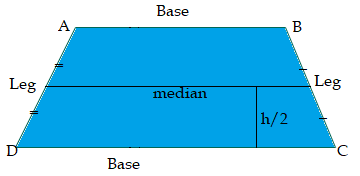

The length of median (m) =

We can calculate the trapezoid area if we know the length of the trapezoid's median and height. It is the median times of height:

A = m * h

Adjacent angles of a trapezoid

The angles formed on the same side of a leg (line) are called adjacent angles, and these angles are supplementary. In the below-mentioned trapezoid diagram, angles ∠A and ∠D are adjacent angles and supplementary. In the same way, ∠B and ∠C are supplementary.

When the sum of two angles became, 180 degrees is called supplementary.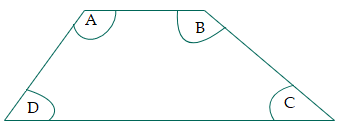

Problem 1: Using the adjacent angles property of trapezoid, find D if A = 125.

According to adjacent angles property of trapezoid A + D = 180

125 + ∠D = 180

∠D = 180 - 125

∠D = 55 degree

Trapezoid vs Trapezium

Trapezoid and trapezium are the swapped definition of the US and UK. According to US definition: a trapezoid has a pair of parallel sides, and according to UK definition: a trapezoid has no parallel sides. On the other hand, according to the US definition: a trapezium has no parallel sides, and according to the UK definition: a trapezium has a pair of parallel sides.