Green's TheoremIn Mathematics, the relationship between geometry and calculus is quite fascinating for one interested. One of the basic theorems that help us understand these two fields, i.e., Geometry and Calculus, is "Green's Theorem;" This Theorem is named after the British mathematician "George Green," who proposed a similar result in 1828. This Theorem is important in vector calculations, providing a profound connection between line and surface integrals. In this article, we will learn about Green's Theorem, its significance, proof, formulas, and applications and conclude with a conclusion. The Concept of Linear IntegralsBefore we learn about Green's Theorem, it is important to understand or get a basic idea of Linear Integral (as it will be used in Green's Theorem). Line integrals are a mathematical tool used to calculate a scalar field along a curve or path in two-dimensional or three-dimensional space; more importantly, they help us to determine how a scalar quantity (such as temperature, density, or velocity) changes along a particular path. Consider a scalar field, represented by a function f (x, y), and a curve C along which we want to calculate the line integral; mathematically, the line integral. "∮Cf. ds" can be expressed as: 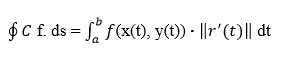
Here, (x(t), y(t)) parametrise the curve C, r(t) = (x(t), y(t)) is the position vector of a point on the curve, and ‖r' (t)‖ is the magnitude of the derivative of the position vector, which shows the displacement along the curve in an infinite manner. Line integrals are mainly useful in physics and engineering, where they are used to calculate quantities such as work done by a force field along a path or the circulation of the velocity of a fluid field around a closed loop. Definition of Green's TheoremGreen's Theorem shows a profound connection between line and surface integrals; it provides a way to evaluate a line integral along a closed curve by considering the properties of the vector field within the region enclosed by that curve. This Theorem is useful because it transforms a complex line integral into a simpler (comparatively) surface integral. In terms of Mathematics, Green's Theorem is stated as follows.Let D be a connected region in the plane, and C be a positively oriented, piecewise-smooth simple curve that bounds D; if F (x, y) = (P (x, y), Q (x, y)) is a vector field whose components have continuous partial derivatives in an open region containing D, then Green's Theorem states that: 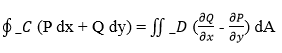
In this Theorem, ∮_C (P dx + Q dy) represents the line integral of the vector field F along the curve C, ∬_D 
Breaking Down Green's TheoremLet us discuss the parts of Green's Theorem with a little explanation.
Proof of Green's TheoremIn this paragraph, we will discuss the proof of Green's Theorem; as per its statement, P and Q are the functions of (x, y) defined on the open region, which contains D and has continuous partial derivatives; so, based on this we have to prove: 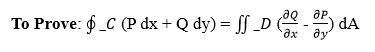
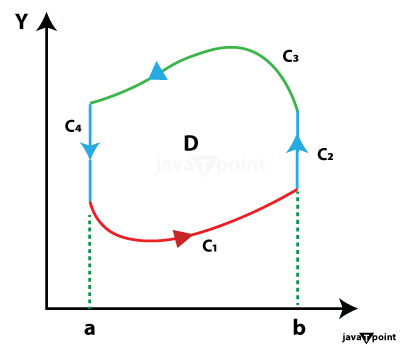
Proof: From the above image, we can say that: 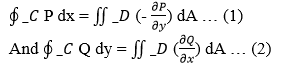
Here, the proof of the first case (left-hand side to right-hand side) of Green's Theorem is solved. As the given diagram has the D region, let it be written as: D = {(x, y) | a ≤ x ≤ b, g1 (x) ≤ y ≤ g2 (x)} Here, g1 and g2 are continuous functions on [a, b]. Now, we will solve for double integral from equation (1) to show that the right-hand side is equal to the left-hand side. 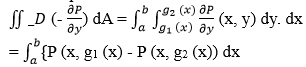
Now, calculate the line integral, which we can see from the diagram: C is divided into C1, C2, C3, and C4. 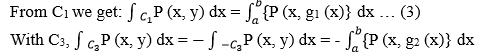
Therefore, C3 goes in the opposite (negative) direction, i.e., from b to a. Now, for C2 and C4 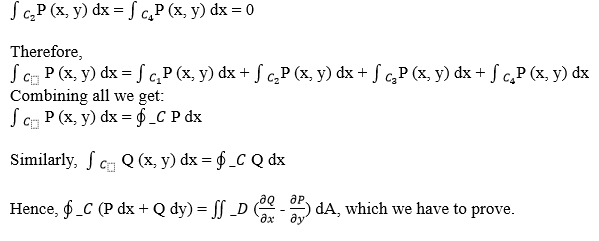
Intuition Behind Green's TheoremThe basic intuition behind Green's Theorem lies in the concept of "conservation of circulation;" it states that the circulation of a vector field around a closed curve is equal to the flux of the curl of that vector field over the region enclosed by the curve. In simpler terms, it quantifies how much the vector field circulates the curve and relates it to the "rotational" behaviour of the field within the enclosed region. Applications of Green's TheoremGreen's Theorem has applications in various fields, including physics, engineering, and fluid dynamics; some of the practical applications are discussed below:
ConclusionGreen's Theorem is a powerful tool that connects line integrals and surface integrals in vector calculus, and it also provides a bridge between geometry and calculus that allows us to calculate line integrals by examining the properties of a vector field within the region enclosed by the curve. This Theorem has many applications in various fields, from physics to engineering, helping us understand the circulation, flux, and behaviour of vector fields; its mathematical formulation and interpretation make it a cornerstone of vector calculus and a valuable tool for solving real-world problems. This Theorem is a powerful tool in vector calculus as it relates line integrals around closed curves to double integrals over the regions enclosed by those curves.
Next TopicCeva's Theorem
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share




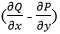 dA represents the surface integral of the curl of F over the region D, and
dA represents the surface integral of the curl of F over the region D, and 




