Ceva's Theorem

Geometry, the study of shapes and their properties, has been a basic and interesting branch of mathematics since ancient times; throughout history, mathematics has discovered many theorems and concepts to solve mathematical problems and understand the world around us in a better way. There are so many different theorems in mathematics, but "Ceva's Theorem" is one of the most remarkable theorems; this theorem is named after the Italian mathematician "Giovanni Ceva." This theorem provides a powerful concept that can be used as a powerful tool for solving complex problems that involve triangles and the relation between their sides; so, in this article, we will get to understand the concept of Ceva's Theorem, knowing its history, definition, and applications in various fields, and concluding with a conclusion.

History

To understand Ceva's Theorem, it's important to understand the conceptual history of this theorem. "Giovanni Ceva" was an Italian mathematician who lived during the late 17^th century, a period when mathematics was undergoing a significant change or transformation. The famous personalities of mathematicians such as Rene Descartes, Pierre de Fermat, and Blaise Pascal shaped mathematical thought; Ceva contributed here.

Ceva's Theorem first appeared in Ceva's 1678 work named "De Lineis Rectis;" in this treatise, Ceva introduced this theorem, which laid the foundation for a deeper understanding of geometric relationships within triangles. Ceva's work was a remarkable addition to mathematics, extending the possibilities of solving complex triangle-related problems.

Some Concepts

Before we get to learn about Ceva's theorem, we have to get a basic understanding of some terms.

• Cevians: Cevians are lines in a triangle that connect the vertices of a triangle to the opposite sides of that triangle; as there are three vertices in a triangle, there are three cevians.
• Cevians Concurrent: This means that these three cevians are intersected at a single point.

Definition of Ceva's Theorem

Consider a triangle ABC with points on each side named F, G, and E on sides BC, AC, and AB, respectively. Then, according to Ceva's Theorem, if three cevians, AF, BG, and CE, are concurrent (i.e., they intersect at a single point), the following condition is true:

(AG) / (GC) * (CF) / (FB) * (BE) / (EA) = 1

The converse of this statement is also true, i.e.,

if (AG) / (GC) * (CF) / (FB) * (BE) / (EA) = 1,

then the lines or cevians AF, BG, and CE are concurrent (i.e., intersecting at a single point).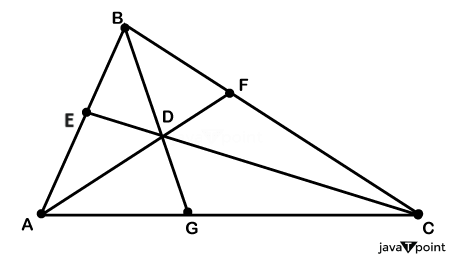

Proof of Ceva's Theorem

We will discuss the proof of this theorem in this paragraph, and we will prove this theorem in the forward statement, i.e., if three cevians, AP, BQ, and CR, are concurrent (i.e., they intersect at a single point), then the following condition is true:

(BP / PC) * (CQ / QA) * (AR / RB) = 1.

Construction: Construct h₁ and h₂, such that they are the perpendicular of triangles ADG, GDC and ABG, BGC, respectively; when h₁ and h₂ are being constructed, we constructed them such that

area of BGC = (1/2) * (GC) * (h₁),

area of ABG = (1/2) * (AG) * (h₁), and

area of DGC = (1/2) * (GC) * (h₂),

area of ADG = (1/2) * (AG) * (h₂).

Proof: Consider triangles ABG and triangle BGC:

Area of ABG / Area of BGC = (1/2) * (AG) * (h₁) / (1/2) * (GC) * (h₁)

Consider triangles ADG and triangle DGC:

Area of ADG / Area of DGC = (1/2) * (AG) * (h₁) / (1/2) * (GC) * (h₁)

On simplifying both the equations, we get:

Area of ABG / Area of BGC = (AG) / (GC) … (1)

Area of ADG / Area of DGC = (AG) / (GC) … (2)

From Equation (1) and (2), we get:

Area of ABG / Area of BGC = Area of ADG / Area of DGC = (AG) / (GC)

Similarly, we can get:

Area of BDA / Area of BDC = (AG) / (GC)

Area of ADC / Area of BDA = (CF) / (FB)

Area of BDC / Area of ADC = (BE) / (EA)

Multiplying all these equations, we get:

[(Area of BDA) * (Area of ADC) * (Area of BDC)] / [(Area of BDC) * (Area of BDA) * (Area of ADC)] = [(AG) * (CF) * (BE) / (GC) * (FB) * (EA)]

In simplification, we get the following:

[(AG) * (CF) * (BE) / (GC) * (FB) * (EA)] = 1

[(AG) / (GC)] * [(CF) / (FB)] * [(BE) / (EA)] = 1, which we have to prove.

Converse Proof: We have [(AG) / (GC)] * [(CF) / (FB)] * [(BE) / (EA)] = 1; here, AF, BG, and CE Cevians are concurrent.

Assuming that Cevians CE and AF intersect at D, let BH be the Cevian passing through D; then, according to Ceva's Theorem, we have:

(AH) / (HC) * (CF) / (FB) * (BE) / (EA) = 1 … (1)

But we have: (AG) / (GC) * (CF) / (FB) * (BE) / (EA) = 1 … (2)

Comparing Equation (1) and Equation (2), we get:

(AH) / (HC) * (CF) / (FB) * (BE) / (EA) = (AG) / (GC) * (CF) / (FB) * (BE) / (EA)

By simplifying, we get:

(AH) / (HC) = (AG) / (GC)

This shows that H and G are the same points, proving that AF, BG, and CE are concurrent, which we have to show.

We have proved Ceva's Theorem in both converse and forward way, so this completes the proof of Ceva's Theorem. This proof shows the basic idea behind Ceva's Theorem: the product of the ratios of segments along the sides of a triangle is equal to 1 if and only if three cevians are concurrent. This theorem gives a powerful tool for solving a wide range of geometric problems involving triangles.

Applications of Ceva's Theorem

Ceva's Theorem has many applications in various branches of mathematics and science; some of the notable examples are discussed below:

1. Trigonometry: Ceva's Theorem can be used to prove trigonometric identities and solve trigonometric equations involving triangles; it provides a better understanding of trigonometric relationships.
2. Geometry: Ceva's Theorem is usually used to solve complex geometric problems that involve the concurrency of cevians within triangles, and it also helps in finding relationships between lengths and angles in triangles.
3. Physics: In physics, Ceva's Theorem can be applied to problems related to forces acting at different angles, and it also helps determine conditions for equilibrium and balance in physical systems.
4. Engineering: Engineers use Ceva's Theorem to analyze and design structures that rely on the equilibrium of forces and moments, and it is particularly valuable in structural engineering and statics.
5. Navigation: Ceva's Theorem can be used in navigation to solve problems related to the intersection of lines of sight from different observation points, and it also helps in determining the location of an object based on multiple observations.
6. Computer Graphics: In computer graphics, Ceva's Theorem calculates intersections and intersections of lines and objects, and it plays an important role in rendering realistic images.

Generalizations and Extensions

Ceva's Theorem is not limited to triangles; it has several generalizations and extensions that apply to other geometric shapes. One such extension is Menelaus' Theorem, which deals with the collinearity of points rather than the concurrency of lines; Menelaus' Theorem is usually seen as a counterpart to Ceva's Theorem and is used to solve problems involving collinear points within triangles.

Another generalization of this theorem is Stewart's Theorem, which focuses on the relationship between a Cevian and the segments it divides within a triangle; Stewart's Theorem provides a formula for calculating the length of a Cevian segment in terms of other segments and the sides of a triangle.

Conclusion

Ceva's Theorem, named after the Italian mathematician "Giovanni Ceva," is a remarkable result in geometry; its statement and versatility applications make it an important tool for solving a wide range of problems in mathematics, physics, engineering, and beyond. The proof of this theorem, which relies on the concept of similar triangles, shows the beauty and power of geometric reasoning.

As we continue to explore the concepts of geometry and its applications, Ceva's Theorem remains a perfect example of how mathematical theorems, that a mathematical concept, can be seen in the world of shapes and relationships. Its relevancy and applicability make it an important concept of geometry that enhances our understanding of the mathematical universe and its connection to the physical world.