Mid Point Theorem

Geometry is a very basic and important branch of mathematics; geometry is a fascinating field where lines, angles, and shapes come together to form the foundation of our understanding of dimension and space. Among the many theorems in geometry that have shaped this field, the mid-point theorem stands as a basic concept that has applications in various geometric fields; so, in this article, we will get to know about the Mid Point theorem, explore its statement and proof, and practical applications, end this article with a conclusion.

Definition

The Mid-Point Theorem is a simple and powerful theorem in geometry that deals with the relationship between the mid-point of a line segment and the line connecting the mid-point to one of the endpoints; it states that:

In a given triangle, if a line segment connects the mid-point of two sides of the triangle, then this line segment is parallel to the third side, and its length is half the length of the third side.

In other words, if we have a triangle and draw a line segment connecting the mid-points of two sides, that line segment will be parallel and equal to half the length of the third side. The theorem is usually represented in an image as follows: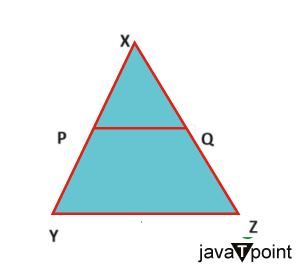

In the diagram above, we have triangle XYZ, and PQ is the line segment connecting the mid-points of sides XY and XZ; according to the Mid-Point Theorem, PQ is parallel to YZ, and its length is half the length of YZ.

Proof of Mid-Point Theorem

In this paragraph, we are going to learn about the proof of the midpoint theorem and also for its converse.

Given: We have a triangle ABC, in which D is the mid-point of the side AB, and E is the mid-point of the side AC.

To Prove: The segment DE is parallel to the segment BC, and DE is equal to half of segment BC, i.e., DE || BC and DE = (1/2) * BC.

Construction: The line segment DE is extended to point F to form another line DF so that DE = EF and then joins the points F and C to form another triangle CEF.

Proof: In triangle AED and triangle CEF,

DE is equal to EF (from construction)

Angle 1 is equal to angle 2 (vertically opposite angle)

AE is equal to CE (as E is the midpoint of AC)

From the triangle, AED is congruent to triangle CEF by the property SAS (Side Angle Side) criteria.

Therefore, angle 3 is equal to angle 4 by the criteria of c.p.c.t

But these are alternative interior angles.

So, AB is parallel to CF, i.e., AB || CF

AD = CF (by criteria c.p.c.t)

But AD = DB (D is the midpoint of AB)

Therefore, BD = CF

In quadrilateral BCFD

In this, BD is parallel to CF, i.e., BD || CF (as AB is parallel to CF, i.e., AB || CF)

BD = CF

So, the quadrilateral BCFD is a Parallelogram, as one pair of opposite sides is parallel and equal.

Therefore, DF is parallel to BC (opposite sides of the parallelogram)

DF = BC (opposite sides of the parallelogram)

As DF is parallel to BC, i.e., DF || BC, DE is parallel to BC, i.e., DE || BC, and DF is equal to BC, but DE is equal to EF.

So, this implies DF is equal to twice of DE.

Also, twice, DE is equal to BC, or DE is equal to half of BC.

Hence, it is proved that the line joining the midpoints of two sides of the triangle is parallel to the third side and is equal to half of the third side.

Converse Proof of Mid-Point Theorem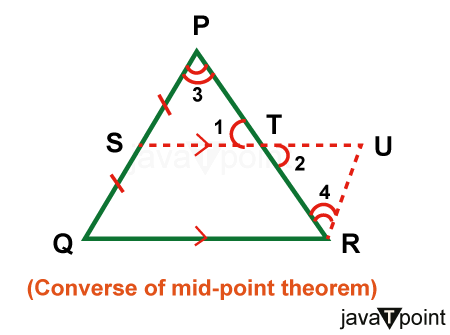

Given: We have a triangle PQR in which S is the midpoint of segment PQ and ST is parallel to QR, i.e., ST || QR.

To Prove: We have to show that T is the midpoint of PR.

Construction: Draw a line from point R to U that is parallel to PQ and then extend ST to connect U.

Proof: As it is given that

ST is parallel to the QR

So, SU || QR

This implies that quadrilateral SURQ is a Parallelogram.

SQ = RU (opposite sides of the parallelogram)

But SQ = PS (S is the midpoint of PQ)

Therefore, PS = RU

In triangle PST and triangle RUT,

Angle 1 is equal to angle 2, i.e., ∠1 =∠2 (vertically opposite angles)

Angle 3 is equal to angle 4, i.e., ∠3 =∠4 (vertically opposite angles)

And PS = RU (Proved above)

This implies triangle PST is congruent to triangle RUT, i.e., △PST ≅ △RUT (by AAS property).

Therefore, PT = RT, which implies T is the midpoint of PR.

Mid-Point Formula

The midpoint of any line segment is the point or coordinate that divides that line segment into two equal parts, so in this paragraph, we will understand the midpoint formula in a 2-D plane.

Consider a line segment in 2-D with end coordinates as X (x₁, y₁) and Y (x₂, y₂), then the formula or coordinates for the midpoint of that line is given by:

Midpoint = {(x₁ + x₂) / 2, (y₁ + y₂) / 2}

Applications of the Mid-Point Theorem

The Mid-Point Theorem has various applications in geometry and mathematics, as well as in real-world problem-solving; here are some notable applications discussed below:

1. Coordinate Geometry: The Mid-Point Theorem is used to find the mid-point of a line segment given the coordinates of its endpoints; this is a valuable tool in coordinate geometry and helps in various geometric calculations.
2. Construction: Architects and engineers use the Mid-Point Theorem to ensure that structures are built accurately and sustainably; for instance, when constructing bridges or buildings, ensuring that support beams are parallel and properly aligned is crucial.
3. Trigonometry: The theorem is used in trigonometric calculations, mainly in the study of vectors and complex numbers, where midpoints play an important role in finding the properties of vectors.
4. Computer Graphics: In computer graphics, understanding mid-points and parallel lines is important for rendering (showing) three-dimensional (3-D) objects on a two-dimensional (2-D) screen.
5. Cartography: Cartographers use the Mid-Point Theorem to create accurate maps by ensuring that lines of longitude and latitude intersect at right angles, among other considerations.
6. Surveying: Surveyors use the theorem to determine distances and angles in land surveying, helping to divide land parcels accurately.
7. Geometry Proofs: The Mid-Point Theorem often serves as a critical step in more complex geometric proofs; it simplifies calculations and is a useful tool in solving Euclidean geometry.

Some Frequently Asked Questions

Q. What do we understand by the Mid-Point Theorem?

Answer: The Midpoint Theorem is a basic concept in geometry that states that in a triangle when we draw a line segment that connects the midpoint of two sides of the triangle, this line segment is not only parallel to the third side but also exactly half the length of that third side. In simpler terms, if you have a triangle and connect the midpoints of two sides, the resulting line is parallel to half as long as the third side of the triangle.

This theorem is particularly valuable in geometry because it provides insight into the relationships between different triangle parts and helps us understand how midpoints play an important part in geometric configurations.

Q. What do we understand by the Midpoint Theorem and its converse?

Answer: The Midpoint Theorem, as we mentioned earlier, states that a line segment connecting the midpoints of two sides of a triangle is parallel to the third side and is half the length of that third side.

The converse of the Midpoint Theorem is another important geometric statement; it states that if we have a line in a triangle that passes through one side's midpoint and is parallel to another side, then that line will divide the third side of the triangle into two equal parts. In other words, if you have a line in a triangle parallel to one side and intersects the other two sides, it will bisect or cut the third side into two equal segments. The Midpoint Theorem and its converse are interrelated concepts that help us explore the properties of triangles and the significance of midpoints within them.

Q. What can we understand by a midpoint in proofs?

Answer: In geometric proofs, the midpoint is defined as the particular point that lies on a line segment that divides that line into two equal parts; in simple terms, it is the point on a line segment that is equidistant from both endpoints of the line. The midpoint is a fundamental concept in geometry and plays an important role in various theorems and proofs, including the Midpoint Theorem.

It is compulsory to identify and work with this point accurately when proving geometric statements with midpoints, as it usually forms the basis for establishing relationships between different parts of geometric figures.

Q. Suppose we have a triangle ABC, and D is any point on BC; let P and Q be midpoints of lines AB and AC, respectively. Show that line PQ equally divides (bisects) AD.

Answer: Given: P and Q are midpoints of the AB and AC sides of the triangle.

Proof: P and Q are midpoints of the AB and AC by the midpoint theorem, so PQ is parallel to BC.

Now, consider the triangle ABD; the line segment PE is parallel to the base BD, and P is the midpoint of AB; so, by the converse of the midpoint theorem, E must be the midpoint of the line AD. So, the line AD is divided into two equal parts: AE and ED.

Therefore, we have proved that PQ bisects AD at E.

Q. Consider a line segment with the coordinates P (8, 9) and Q (6, 7), and find the midpoint of this line segment.

Answer: As we have end coordinates P (8, 9) and Q (6, 7), we have to put these values in the midpoint formula.

As, Midpoint = {(x₁ + x₂) / 2, (y₁ + y₂) / 2}

This implies (x₁, y₁) = (8, 9) and (x₂, y₂) = (6, 7)

Midpoint = {(8 + 6) / 2, (9 + 7) / 2} = (14 / 2, 16 / 2)

Midpoint = (7, 8)

So, the midpoint coordinates of the line are (7, 8).

Conclusion

The Mid-Point Theorem is a basic concept in geometry that provides a simple and important way to understand the relationship between mid-points of line segments and the lines that are connecting them. Its proof is also simple, which shows the beauty of geometry and its applications in various fields other than mathematics, from architecture and engineering to computer graphics and cartography. Whether one is a student studying geometry or a professional using geometric principles in their work, the Mid-Point Theorem is always a valuable tool in our mathematical toolkit, enabling us to explore and understand the world of shapes, lines, and angles with greater precision and insight.