Area of a Cylinder

In this section, we will learn cylinder definition, formula derivation, and area of cylinder formula along with examples in detail.

Cylinder

A cylinder is a three-dimensional solid shape. It has two parallel faces that have congruent circles. It has a curved surface. The perpendicular distance between the two bases is the height of the cylinder.

Area of Cylinder formula

OR

Where:

π is a constant whose value is 3.14.

r is the radius.

h is the height of the cylinder

Types of Cylinder

There are two types of cylinder:

• Right Cylinder: If the bases of the cylinder are at the exact position and the axis is at a right angle to the base is called the right cylinder.
• Oblique Cylinder: If the bases of the cylinder are not at the position and the axis is not a right angle to the base, it is called an oblique cylinder.

Derivation

A cylinder is made up of two circles and a rectangle. If you want to derive the formula of area of the cylinder, follow the steps given below:

• Divide the cylinder into three parts: two circles and a rectangle.
• Unroll the sides that form a rectangle.

Calculate the area of each circle separately. We know that the area of the circle is πr². Adding the area of both circles we get (πr² + πr² = 2πr²).

Calculate the area of the rectangle that is width times height. Where h is height, and the length of the cylinder is the distance around the circle. It means it is the circumference of the circle that is 2πr. Hence the area of the rectangle will be 2πr*h.

Now add the area of the circle that is 2πr² and the area of a rectangle that is 2πrh.

Area of cylinder (A) = 2πr² + 2πrh

OR

Area of cylinder (A) = 2πr (r + h)

Where:

π is a constant

r is the radius

h is the height of the cylinder

Examples

Example 1: If the diameter of a cylinder is 15 cm and the height is 7 cm. Find the surface area of the cylinder.

Solution:

We have given, diameter (d) = 15 cm

height (h) =7 cm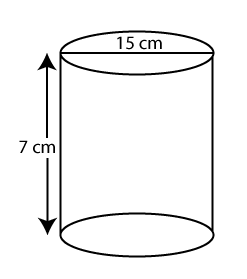

we know that, radius is half of the diameter.

r = d/2

r = 15 / 2 = 7.5 cm

We know that,

Area of cylinder (A) = 2πr (r + h)

A = 2 * 3.14 * 7.5 (7.5 + 7)

A = 682.95 cm²

The area of the cylinder is 682.95 cm².

Surface area of the hollow cylinder

Example 2: The following figure shows a pipe. The internal and external radius of the pipe is 4 cm and 4.4 cm, respectively. The pipe is 9 cm is long. Find the total surface area of the pipe.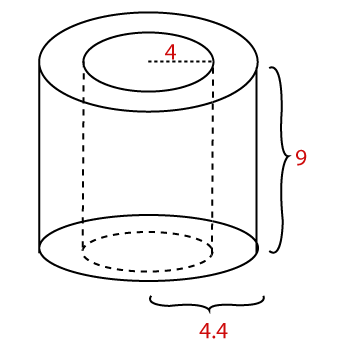

Solution:

In this question, we have given two radiuses, internal and external. The r represents the internal radius, and R represents the external radius.

We have given,

r = 4 cm, R = 4.4 cm and h = 9 cm

Total surface area of the pipe (A) = area of internal circle + area of external circle + area of two circles

A=2πrh+ 2πRh+2(πR²- πr²)

A = 2π.4.9 + 2π.(4.4).9 + (2. (π.(4.4²)-π.4²))

A = 72π + 79.2π +(2. (19.36π - 16π))

A = 72π + 79.2π +(2. (3.36π))

A = 72π + 79.2π + 6.72π

A = 157.92π

A = 157.92 * 3.14

A = 495.86 cm²

The area of cylinder is 495.86 cm².