What is 30% of 100?

Percentage is a fundamental concept of mathematics that is not only important in Mathematics but also important in our daily lives. It helps us express fractions and proportions simply, making it easier to compare and comprehend these values. One of the common examples that arise in many scenarios is calculating 30 percent, so, in this article, we will get to know the concept of 30 percent, understand the 30 percent of 100, and get to know the applications and conclusion in the end.

Understanding Percentages

Before we learn about the calculation of 30 percent of 100, let's ensure we have a good knowledge of the concept of percentages. A percentage is a way of expressing a proportion or a fraction out of 100. The symbol "%" represents a percentage and is read as "percent." Percentages are commonly used to compare values and make relative statements.

Calculating 30% of 100

To calculate 30 percent of 100, we need to follow a simple process. Since "30%" means 30 out of 100, we can express it as a fraction: 30 / 100. To find 30% of 100, multiply the fraction 30 / 100 by 100.

Let's Break Down the Calculation Step-by-Step

We will learn how to calculate 30% of 100 with the help of some simple steps, which are explained in the following lines.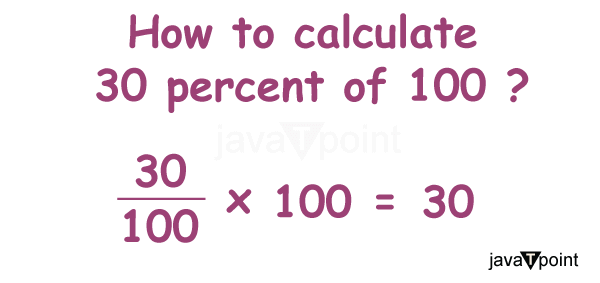

Step 1. First, write the product of both numbers, i.e., 30% and 100, as shown below.

= 30% * 100

Step 2. As we know, the meaning of percentage is the 100^th part of a number or anything so we can replace the "%" with (1 / 100).

= 30% * 100 = (30 / 100) * 100

Step 3. Using the rules of multiplication and simplification, we get the following:

=30% * 100 = (30 / 100) * 100

= 3,000 / 100

= 30

Applications of Percentages

In the following discussion, we will learn about some percentages' applications connecting with real-life examples.

1. Shopping Discounts: Imagine you visit a store offering a 30 percent discount on a $100 item. You must determine 30% of $100 to calculate the amount you save. Using the calculation:

30 / 100 = 0.3

0.3 × 100 = 30

Therefore, you will save $30 on the $100 item; you must pay only $70.

2. Exam Scores: In a school, a student scores 30 out of 100 on a math test. To determine the percentage score of that student, we need to calculate what proportion 30 represents out of 100. Using the formula:

30 / 100 = 0.3

0.3 × 100 = 30%

Therefore, the student scored 30% on the math test.

3. Stock Market Performance: Suppose you invest $100 in a stock, and it increases by 30 percent. To calculate the new value of your investment, you need to find 30 percent of $100. Using the method explained above:

30 / 100 = 0.3

0.3 × 100 = $30

The stock's value increased by $30, making your investment worth $130.

4. Probability: Percentages are used in probability calculations; if there is a 35 percent chance of rain today, it means that out of every 100 similar weather situations, it would be expected to rain in 35.

5. Statistical Analysis: Percentages are widely used in statistical analysis to interpret data; they help in comparing proportions, calculating growth rates, and understanding distributions.

Some Solved Examples

Q. What is 30% of 10?

Solution:

Step 1. 30% * 10

Step 2. 30% * 10 = (30 / 100) * 10

Step 3. 30% * 10 = (30 / 100) * 10 = 300 / 100 = 3

Q. What is 30% of 50?

Solution:

Step 1. 30% * 50

Step 2. 30% * 50 = (30 / 100) * 50

Step 3. 30% * 50 = (30 / 100) * 50 = 1,500 / 100 = 15

Q. What is 75% of 30?

Solution:

Step 1. 75% * 30

Step 2. 75% * 30 = (75 / 100) * 30

Step 3. 75% * 30 = (75 / 100) * 30 = 2,250 / 100 = 22.5

Q. What is 28% of 100?

Solution:

Step 1. 28% * 100

Step 2. 28% * 100 = (28 / 100) * 100

Step 3. 28% * 100 = (28 / 100) * 100 = 2,800 / 100 = 28

Q. What is 30% of 20?

Solution:

Step 1. 30% * 20

Step 2. 30% * 20 = (30 / 100) * 20

Step 3. 30% * 20 = (30 / 100) * 20 = 600 / 100 = 6

Q. What is 30% of 200?

Solution:

Step 1. 30% * 200

Step 2. 30% * 200 = (30 / 100) * 200

Step 3. 30% * 200 = (30 / 100) * 200 = 6,000 / 100 = 60

Conclusion

Percentages are a fundamental concept of Mathematics that allows us to express proportions and make comparisons. In our case of calculating 30% of 100, we multiply the total value by 30% (0.3) to obtain the result, i.e., 30. This knowledge is sound in mathematics and applicable in various real-world scenarios, such as sales, gratuity, and financial investments. By understanding percentages and proportions, we can improve our problem-solving abilities and make informed decisions in various aspects of life.