Area of Square

A square is a closed figure on a 2D plane that has four parallel sides. The property of the square is that all the sides (breadth and length) must have equal length. In a square, each angle is of 90�.

In this section, we will learn area of square formula, and how to find area of a square.

Area of Square

The area is the region covered by the four-sides. In other words, the number of square units it takes to fill a square completely.

In the following image, we have divided a square into five rows and five columns. It makes the multiple small squares that completely fills the square. Hence 25 small squares represent the area of the square.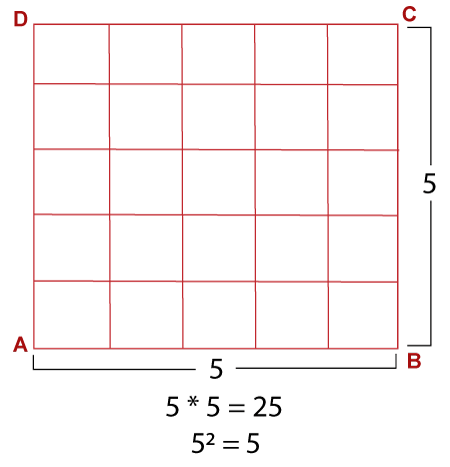

Area of Square Formula

To calculate the area of a square, multiply the base to itself. In short, the square of the side is the area of the square.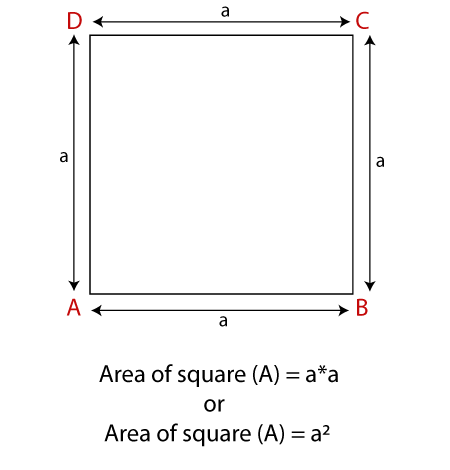

Where a is the side of a square whose length is a.

When the diagonal is given

We can also calculate the area of a square if the length of the diagonal is given. The area is half the product of the diagonals. Both the diagonals are equal length.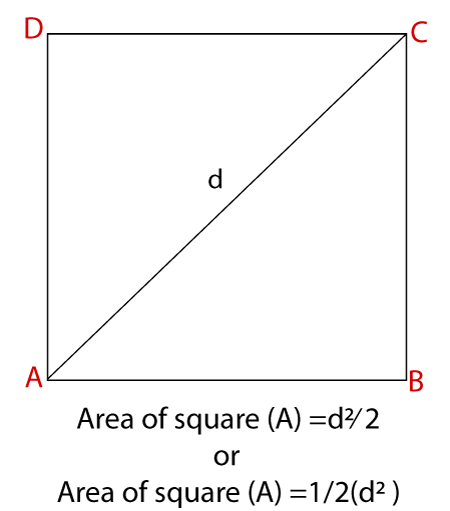

Where d is the length of either diagonal.

Derivation

Consider a square as a rectangular shape whose length is l and breadth are b. According to the area of rectangle formula:

Where,

• A is the area
• l is length
• b is breadth

Suppose that a side of a square is a. Then the area of the square will be:

A = a*b

We know that all sides of the square are equal length. Then,

A = a*a

A = a²

Examples

Example 1: Find the area of a square whose side length is 12 cm.

Solution:

We have given that a side of the square is 12 cm.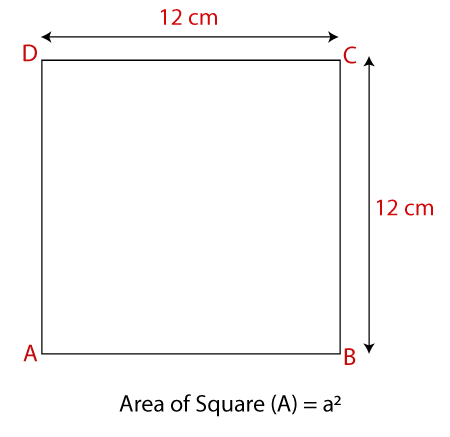

We know that

Area of square (A) = a²

A = 12²= 144 cm²

The area of the square is 144 cm².

Example 2: The perimeter if a square is 24 yd, calculate the area of the square.

Solution:

Given, perimeter (P) = 24 yd

We know that

Perimeter of the square (P) = 4a

Where a is the length of the side.

Putting the value of P in the above formula we get:

We know that,

Area of square (A) = a²

Substitute value and simplify, we get:

A = 6*6 = 36 yd²

The area of the square is 36 yd².

Example 3: Find the area of the given square.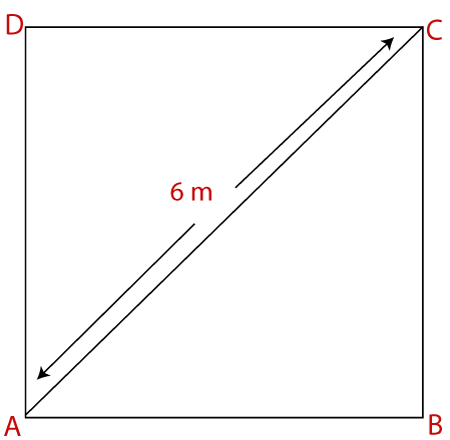

Solution:

Given, length of diagonal (d) = 6 m

We know that,

Area of square (A) = d²/2

Putting the value of d in the above formula, we get:

A = (6)²/2

A = 36/2

A = 18 m²

The area of the square is 18 m².