What is 10 to the 3rd Power?

Exponentiation is a fundamental mathematical process in various fields of study, ranging from elementary arithmetic to sophisticated scientific research. It allows us to represent repeated multiplication efficiently and concisely. The exponent, the Power, determines how many times the base is multiplied by itself. In the example of 10^3, the base is ten, and the exponent is three, implying that we multiply ten by itself three times.

Calculating 10 to the 3^RD Power

The value of 10^3 is 1,000. This means that when we multiply ten by itself three times, the product is 1,000. Another way to express this is:

10^3 = 10 × 10 × 10 = 1,000.

To understanding the magnitude of 10^3 better, let's examine some comparisons and situations in which this value is pertinent. It's crucial to remember that 10^3 corresponds to one thousand. This is because under the International System of Units (SI), the prefix "kilo-" represents one thousand.

10^3 is considered a large number. Considerations of quantities involving a thousand or a significant portion of a total are important when dealing with values like 10^3.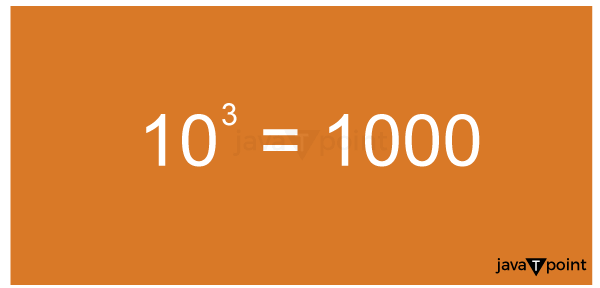

Significance of 10^3

Powers of Ten: The importance of 10^3 becomes clear when considering power of ten. Each successive power of ten is obtained by multiplying the previous power by a factor of ten. For instance, 10^0 equals 1, 10^1 = 1 × 10 = 10, 10^2 = 10 × 10 = 100, 10^3 = 100 × 10 = 1,000, etc. The powers of ten are frequently utilized in scientific notation, engineering calculations, and exponential growth models.

Decimal System: The decimal system, which relies on powers of ten, is the most used number system. Each place value can be expressed by multiplying a natural number with a power of ten. For example, the unit place is denoted by 10^0, the tens place is denoted 10^1, the hundreds place is denoted 10^2, and the thousands place is denoted by 10^3. Understanding the powers of ten aids in our understanding of the structure and magnitude of numbers in the decimal system.

The Metric System: The Metric System widely used in research and everyday life, is based on powers of ten. 10^3 corresponds to the kilo-prefix, which means one thousand. It is used in several metric measures, including the kilometer (km), kilogram (kg), kilowatt (kW), and so on. These units make computations easier and give a standardized measuring system.

Time and Frequency: The idea of 10^3 is important in many scientific domains, such as physics and engineering, when dealing with time and frequency. For example, one kilohertz (kHz) equals 10^3 cycles or oscillations per second. This unit is widely employed in telecommunications, electronics, and signal processing.

Orders of Magnitude: Orders of magnitude are represented by powers of ten, allowing you to compare the scale or size of different things. Each increment in power signifies a tenfold increase in magnitude. For example, if we compare the number 10^3 to the number 10^6, we can claim that the latter is three orders of magnitude greater. Orders of magnitude are important in scientific study, astrophysics, and many other domains.

Exponential Growth and Decay: Exponential functions are a basic aspect of mathematics and have several applications. One such function involves Euler's number, denoted as e, which is approximately equal to 2.71828 raised to any real number. Exponential growth or decay with a base of 10 is found in various instances. The Power of ten is crucial when analyzing exponential systems that demonstrate rapid growth or fall.

Logarithms: Logarithms are mathematical functions that can assist us in solving exponential equations and performing difficult computations. In scientific and technical computations, the logarithm base 10, commonly known as the common logarithm or logarithm to the base 10, is frequently employed. It gives a method for determining the exponent required to obtain a given number when the base is 10. For example, log₁₀(1,000) = 3, which means that 10 to the power 3 equals 1,000.

Conclusion

We can better understand the size, quantity, and relationships between numbers in the real world by grasping the notion of 10^3 and its significance in many contexts. It enables efficient representation, simplifies computations, and facilitates comparisons of quantities across various fields of research and applications.

Exponentiation and powers of ten are fundamental concepts in mathematics, science, and daily life. They allow us to swiftly represent and manipulate numbers, providing a powerful tool for comprehending the world around us.