Volume of a CubeIn this section, we will learn the formula of volume of a cube and how to find the volume of a cube. A cube is a three-dimensional solid shape whose length, breadth and height are equal. It has six square faces. Each face of a cube has a side of equal length. Dice is the best example of a cube. The following figure shows the shape of a cube. 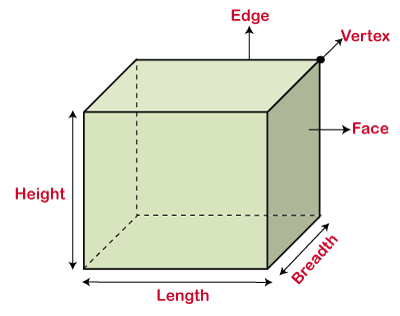
The volume of a CubeThe number of cubic units that a cube occupied is called the volume of the cube. It is the product of length, breadth, and height. In other words, it is the cube of one side. It is denoted by the letter V. The Formula of Volume of a cubeMultiply the length (l), breadth (b), and height (h) together to get the volume of a cube. Remember that length, breadth, and height must be equal in size.
The Volume of a Cube (V)=length×breadth×height
Or
The Volume of a Cube (V)=l×b×h
Suppose the length, breadth, and height of a cube is a, the volume will be: 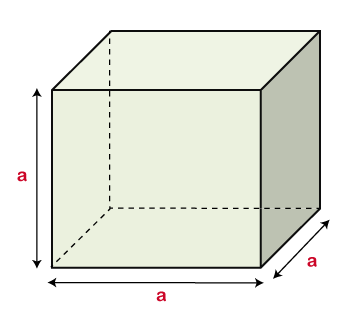
The Volume of a Cube (V)=a×a×a
Or
The Volume of a Cube (V)=a3
Where: V: is the volume a: is a side of the cube When the length of the diagonal is given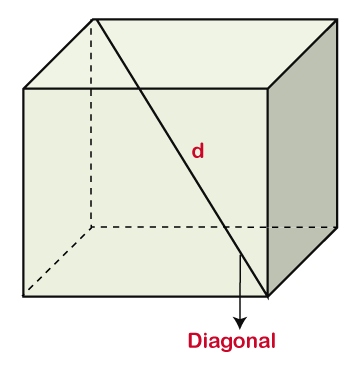
Suppose, the diagonal length is d, then the volume of the cube will be: 
Where: V: is the volume d: is the length of diagonal Derivation of the FormulaThe space occupied by a solid object is called the volume of that object. We know that all the sides (edges) in a cube are of equal length. Therefore, the formula of the volume of a cube can be derived as follows:
Let's see how to find the volume of the cube. Example 1: A side of a cube is 9 cm. Find the volume of a cube. Solution: Given, side = 9 cm volume (V)=? 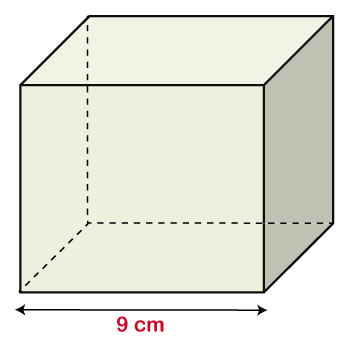
According to the formula:
The volume of a cube (V) = a3
Putting the value of side in the above formula, we get: V= 93
Hence, the volume of the cube is 729 cm3. Example 2: The diagonal length of a gift box is 7 cm. Find the volume of the box. Solution: Given, diagonal length (d) = 7 cm volume (V) =? 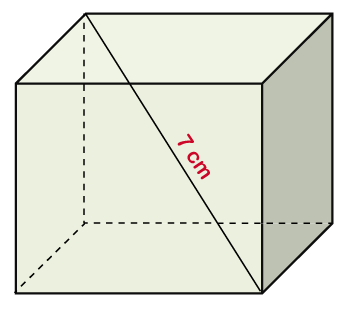
According to the formula: 
Putting the value of d in the above formula, we get: 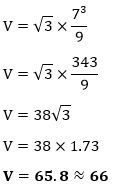
Hence, the volume of the cube is 66 cm3. Example 3: The volume of dice is 64 cm3. Find the length of the edge of the dice. Solution: Given, volume (V) = 64 cm3 side (a)=? According to the formula:
The volume of a cube (V) = a3
Putting the value of side in the above formula, we get: 64= a3 Hence, the length of an edge of the dice is 4 cm. Example 4: Find the volume of the cube given below. 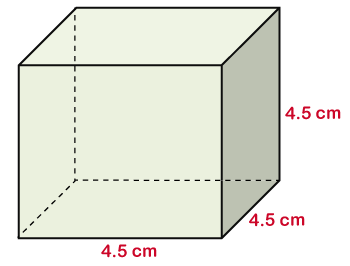
Solution: Given, side (a) = 4.5 cm volume (V)=? According to the formula:
The volume of a cube (V) = a3
Putting the value of side in the above formula, we get: V = (4.5)3 Hence, the volume of the given cube is 91.13 cm3.
Next TopicGreatest Common Factor
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









