What Is 1 Mod 4

In modular arithmetic, congruence relations play a vital role in understanding the patterns and relationships among numbers. One such congruence relation is "1 mod 4." This article will explore the concept of 1 mod 4 and delve into its properties, applications, and significance in various mathematical contexts. By the end, you will comprehensively understand this intriguing mathematical relationship.

Understanding Modular Arithmetic

Before we dive into the specifics of 1 mod 4, let's first grasp the fundamentals of modular arithmetic. In this branch of mathematics, numbers are divided into equivalence classes based on their remainders when divided by a given modulus. The modulus acts as a fixed number, determining the size of each equivalence class.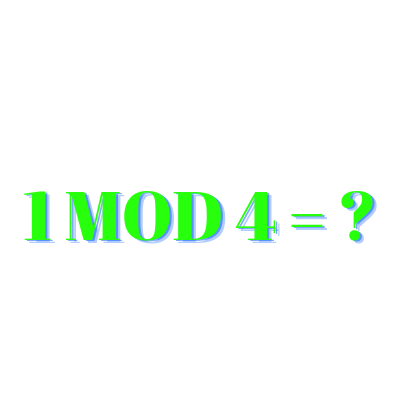

The notation "a ≡ b (mod m)" denotes that a and b have the same remainder when divided by m. In the case of "1 mod 4," it means that numbers that leave a remainder of 1 when divided by 4 falls into the same equivalence class.

Exploring the Congruence Relation 1 mod 4

In the context of 1 mod 4, we encounter a fascinating pattern when examining the numbers in this equivalence class. Consider the following sequence of numbers:

1, 5, 9, 13, 17, 21, 25, 29, 33, 37, ...

Notice that each number in the sequence is 4 units greater than the previous one. This pattern persists indefinitely. We can express this pattern algebraically as follows:

1 + 4k, where k is an integer.

Properties of 1 mod 4

Addition and Subtraction: When we perform addition or subtraction operations involving numbers in the congruence relation 1 mod 4, the result stays within the same equivalence class. For example, (1 + 5) mod 4 = 2, and (13 - 9) mod 4 = 4.

• Multiplication: When we multiply a number in the equivalence class 1 mod 4 by another number, the result remains in the same class. For instance, (1 * 5) mod 4 = 1, and (9 * 13) mod 4 = 1.
• Division: Division in modular arithmetic can be a bit more complex. However, it is important to note that not all numbers in the congruence relation 1 mod 4 have a multiplicative inverse within the same equivalence class. In other words, not all numbers in this class can be divided evenly by another number in the same class.

Applications of Modular Arithmetic

• Cryptography: Modular arithmetic, including the congruence relation 1 mod 4, finds extensive applications in cryptography algorithms. Cryptographic systems utilize modular arithmetic to ensure secure communication and data encryption. Understanding congruence relations helps in the design and analysis of these cryptographic systems.
• Number Theory: Congruence relations are fundamental to number theory, which deals with the properties and relationships of integers. The study of congruence relations enables researchers to investigate prime numbers, modular exponentiation, and other intricate number-theoretic concepts.
• Computer Science: Modular arithmetic, including 1 mod 4, is heavily employed in computer science and programming. It enables efficient computation of large numbers, handling of cyclic data structures, and various algorithms that require periodicity or repetitive patterns.
• Sequences and Series: Congruence relations often appear in the study of sequences and series. The congruence relation 1 mod 4 is no exception. Analyzing this relation allows mathematicians to identify patterns, derive general formulas, and make predictions about the behavior of sequences and series.

Significance and Further Exploration

The congruence relation holds a significant place in modular arithmetic and various mathematical fields. It's a predictable pattern and algebraic representation makes it a valuable tool for solving problems, establishing connections, and uncovering hidden relationships.

Exploring congruence relations like 1 mod 4 can lead to further investigations and discoveries. Mathematicians often generalize these relations to higher moduli or explore different congruence classes to unveil new patterns and insights. Such explorations can contribute to advancements in number theory, cryptography, and computer science.

Conclusion

The congruence relation 1 mod 4 provides a fascinating insight into the world of modular arithmetic. Understanding its properties, applications, and significance not only enhances our knowledge of mathematics but also enables us to make connections with other fields such as cryptography, number theory, and computer science. By delving into the patterns and behaviors of numbers in this equivalence class, we unravel the intricacies of modular arithmetic and unlock new avenues for exploration. So, the next time you encounter the notation "1 mod 4," remember that it represents a world of patterns waiting to be discovered and understood.