Volume of a SphereA sphere is the locus of points. The points have equidistant from the center. It is symmetrical figure. It has no corners. In this section, we will learn the volume formula, and also learn how to find the volume of a sphere. DefinitionA sphere is a round shape solid object in three-dimensional space. It can be defined as the set of points that are all at the same distance from a given point (center). The perfect example of the sphere is the globe and ball. The following figure shows a sphere shape whose radius is r, and the diameter is d. 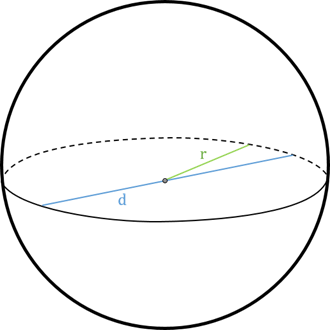
There is a slight difference between a sphere, and a circle is that a circle is a two-dimensional shape while the sphere is a three-dimensional shape. Volume of Sphere FormulaWhen radius (r) is Given:
Where: V: is the volume of the sphere π:is a constant whose value is 3.14 or 22/7 r: is the radius of the sphere When diameter (d) is Given:
Where: V: is the volume of the sphere π:is a constant whose value is 3.14 or 22/7 d: is the diameter of the sphere When Circumference (C) is Given:
Where: V: is the volume of the sphere C: is the circumference of the sphere π:is a constant whose value is 3.14 or 22/7 r: is the radius of the sphere When Surface Area (A) is Given:
Where: V: is the volume of the sphere A: is the surface area of the sphere π:is a constant whose value is 3.14 or 22/7 Let's see some examples based on the above formulas. When the radius is given in the question: Example 1: Find the volume of a sphere whose radius is 7 inches. Take π=3.14. Solution: Given, radius (r) = 7 inches π=3.14 volume (V) =? 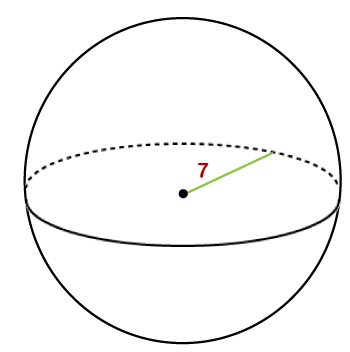
According to the formula: 
Putting the value of r in the above formula, we get: 
Hence, the volume of the sphere is 1436.02 inches3. Example 2: Find the volume of a sphere whose radius is 12 cm. Take Solution: Given, radius (r) = 12 cm
volume (V) =? 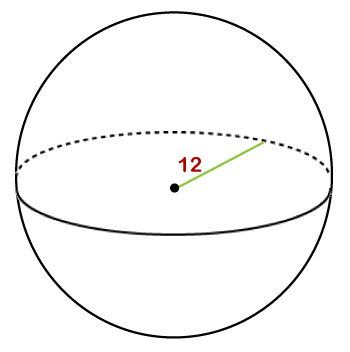
According to the formula: 
Putting the value of r in the above formula, we get: 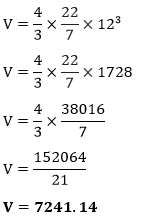
Hence, the volume of the sphere is 7241.14 cm3. When the diameter is given in the question: Example 3: The diameter of a ball is 18 cm. Find the volume of the ball. Take Solution: Given, diameter (d) = 18 cm
volume (V) =? 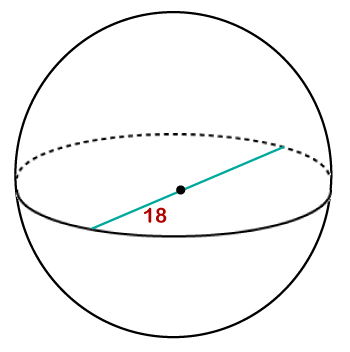
According to the formula: 
Putting the value of d in the above formula, we get: 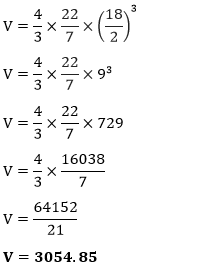
Hence, the volume of the ball is 3054.85 cm3. Example 4: The diameter of a globe is 6 feet. Find the volume of the globe. Solution: Given, diameter (d) = 6 ft π=3.14 volume (V) =? 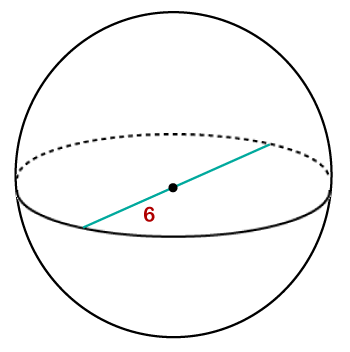
According to the formula: 
Putting the value of d in the above formula, we get: 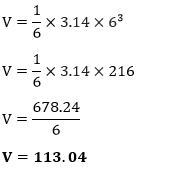
Hence, the volume of the globe is 113.04 ft3. When circumference is given in the question: Example 5: The circumference of a ball is 31.4 cm. Find the volume of the ball. Solution: Given, circumference (C) = 31.4 ft π=3.14 volume (V) =? 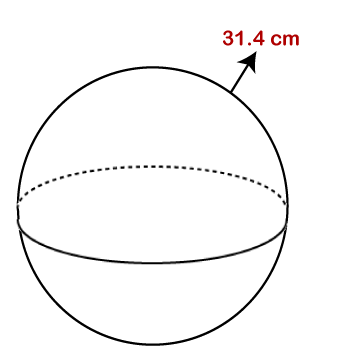
According to the formula: 
In the question, radius (r) is not given, but it is required. So, first, we will find the radius with the help of circumference. We know that: Circumference (C)= 2πr Since, 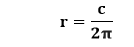
Putting the value of C in the above formula, we get: 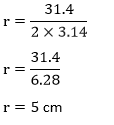
Now, we will put the value of circumference and radius in the volume formula. 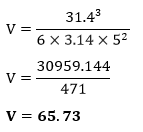
Hence, the volume of the ball is 65.73 cm3. When the surface area is given in the question: Example 6: If the surface area of the sphere is 172 cm2, find the volume of the sphere. Solution: Given, surface area (A) = 172 cm2 π=3.14 volume (V) =? According to the formula: 
Putting the values in the above formula, we get: 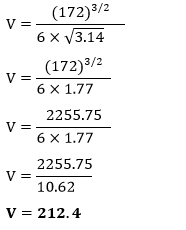
Hence, the volume of the sphere is 212.4 cm3. Example 7: The surface area of a football is 96 cm2. Find the volume of football. Solution: Given, surface area (A) = 96 cm2 π=3.14 volume (V) =? According to the formula: 
Putting the values in the above formula, we get: 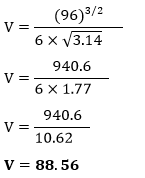
Hence, the volume of football is 88.56 cm3. Example 8: Find the volume of the figure given below. 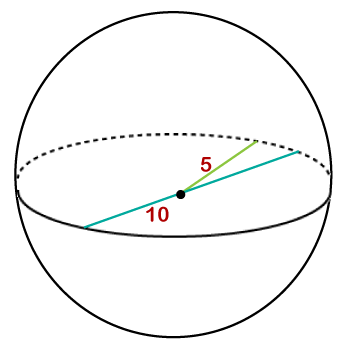
Solution: Given, radius (r) = 5 inches π=3.14 volume (V) =? According to the formula: 
Putting the value of r in the above formula, we get: 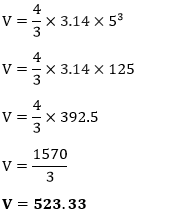
Hence, the volume of the given sphere is 523.33 inches3.
Next TopicVolume of a Rectangular Prism
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





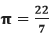 .
.




