What is 15% of 100?

The percentage is an important concept not just in Mathematics but also in our daily lives; like influencing various aspects of finance, mathematics, and real-world scenarios. With the help of percentages, we can express proportions and make comparisons easily. In this article, we will get to learn the concept of percentages, we will also learn "What is 15% of 100" through a comprehensive discussion, and also learn about the applications of percentages.

What is the Percentage?

The word "percentage" is the combination of two Latin words that are "Per" and "Centum," each having different meanings. "Centum" means "hundred," while "Per" means "by." By combining these words, we can define "percentage" as a value that is represented by a hundredth of its total value. With the help of this definition, we can describe a percentage as the value of something compared to one-hundredth of its total value.

During our time as students, we often calculated our overall marks out of the total marks. This involved summing up the marks obtained in various subjects, dividing them by the total marks of all subjects, and then multiplying the result by 100 to obtain a percentage.

For Example: Let us consider that we got 98 marks in Physics out of 100, 93 marks in chemistry out of 100, 74 marks in Mathematics out of 100, 97 marks in Biology out of 100, and 92 marks in Physical Education out of 100.

When we sum up all the marks of each subject, we get 454, divide it by 500, the total marks, and multiply it by 100 to get the marks percentage.

(454 / 500) * 100 = 90.8 %

So that child got 90.8 % in his examination.

What is the Actual Meaning of 15% of 100?

In particular, 15% of 100 is 15.

We can understand this concept by simply assuming 100 as 100 equal parts and objects, and can assume anything; then 15 parts or objects from those 100 equal parts are considered as 15%, for our case, 15 is the answer.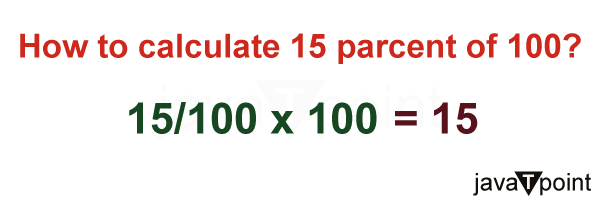

Steps to Calculate 15% of 100

We will learn how to calculate 15% of 100 with the help of some simple steps, which are explained in the following lines.

Step 1. First of all, write the product of both numbers, i.e., 15% and 100, as shown below.

15% * 100

Step 2. As we know, the meaning of percentage is the 100^th part of a number or anything so we can replace the "%" with (1 / 100).

15% * 100 = (15 / 100) * 100

Step 3. Using the rules of multiplication and simplification, we get the following:

= 1500 / 100

= 15

Suppose the whole pie chart represents 100 values. To determine 15% of 100, we calculate 15. The section of the chart occupied by the 15 values represents 15% of the total. The remaining portion of the chart represents 85% of the 100 values. Since 100 is the total value, the entire pie chart represents (whole) 100% of it.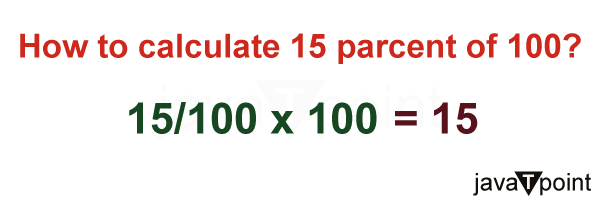

Applications of Percentages

1. Discounts and Sales: Percentages are usually used to indicate discounts and sales on objects in shops or malls; for instance, a store may offer a 15% discount on a product priced at 100 units. Using the calculation, we can determine the discount, i.e., 15 units, and the price of the product is 85 units.

2. Taxes and Tips : Percentages are frequently used to calculate taxes and tips in the service industry. Consider an example, if a restaurant bill is 100 units and the tax rate is 15%, the tax amount would be 15 units. Similarly, if you want to tip 15% on a 100-unit bill, the tip amount would be 15 units.

3. Interest Rates: Percentages play an important role in financial transactions, particularly when it comes to interest rates; for example, if you borrow 100 units from a bank with an annual interest rate of 15%, you would need to pay back to the bank of the amount 115 units after a year.

4. Statistical Analysis: Percentages are widely used in statistical analysis to interpret data; they help in comparing proportions, calculating growth rates, and understanding distributions.

Some Solved Examples

Q. What is 5% of 100?

Solution:

Step 1. 5% * 100

Step 2. 5% * 100 = (5 / 100) * 100

Step 3. 5% * 100 = (5 / 100) * 100 = 500 / 100 = 5

Q. What is 21% of 100?

Solution:

Step 1. 21% * 100

Step 2. 21% * 100 = (21 / 100) * 100

Step 3. 21% * 100 = (21 / 100) * 100 = 2100 / 100 = 21

Q. What is 17% of 200?

Solution:

Step 1. 17% * 200

Step 2. 17% * 200 = (17 / 100) * 200

Step 3. 17% * 200 = (17 / 100) * 200 = 3,400 / 100 = 34

Q. What is 88% of 9100?

Solution:

Step 1. 88% * 9100

Step 2. 88% * 9100 = (88 / 100) * 9,100

Step 3. 88% * 9100 = (88 / 100) * 9,100 = 8,00,800 / 100 = 8008

Q. What is 39% of 500?

Solution:

Step 1. 39% * 500

Step 2. 39% * 500 = (39 / 100) * 500

Step 3. 39% * 500 = (39 / 100) * 500 = 19,500 / 100 = 195

Q. What is 20% of 1000?

Solution:

Step 1. 20% * 1000

Step 2. 20% * 1000 = (20 / 100) * 1000

Step 3. 20% * 1000 = (20 / 100) * 1000 = 20,000 / 100 = 200

Q. What is 20% of 100?

Solution:

Step 1. 20% * 100

Step 2. 20% * 100 = (20 / 100) * 100

Step 3. 20% * 100 = (20 / 100) * 100 = 2,000 / 100 = 20

Q. What is 21% of 5000?

Solution:

Step 1. 21% * 5000

Step 2. 21% * 5000 = (21 / 100) * 5000

Step 3. 21% * 5000 = (21 / 100) * 5000 = 1,05,000 / 100 = 1,050

Q. What is 20% of 50?

Solution:

Step 1. 20% * 50

Step 2. 20% * 50 = (20 / 100) * 50

Step 3. 20% * 50 = (20 / 100) * 50 = 1,000 / 100 = 10

Conclusion

Percentages are a fundamental or basic concept of Mathematics that allows us to express proportions and make comparisons. In our case of calculating 15% of 100, we multiply the total value by 15% (0.15) to obtain the result, i.e., 15. This knowledge is not only useful in mathematics but also applicable in various real-world scenarios, such as sales, gratuity, and financial investments. By understanding percentages and proportions, we can improve our problem-solving abilities and make informed decisions in various aspects of life.