Square 1 To 30
Squares, the fundamental mathematical concept, hold a significant place in the realm of numbers. From the earliest days of mathematics, humans have been captivated by the patterns and properties exhibited by the squares of numbers. In this article, we embark on a journey through the world of squares, focusing specifically on the squares of numbers ranging from 1 to 30.
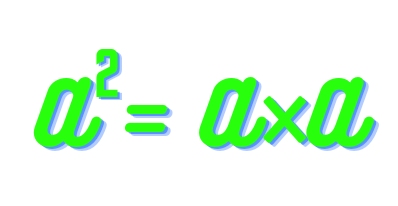
Squaring a number involves multiplying it by itself, resulting in a product known as its square. For example, squaring 3 yields 9 (32 = 9), and squaring 7 gives us 49 (72 = 49). By examining the squares of numbers in this range, we aim to not only showcase the numerical outcomes but also shed light on the underlying relationships and principles at play.
Squares of Numbers 1 to 30
| 12= 1 |
112= 121 |
212= 441 |
| 22= 4 |
122= 144 |
222= 484 |
| 32= 9 |
132= 169 |
232= 529 |
| 42= 16 |
142= 196 |
242= 576 |
| 52= 25 |
152= 225 |
252= 625 |
| 62= 36 |
162= 256 |
262= 676 |
| 72= 49 |
172= 289 |
272= 729 |
| 82= 64 |
182= 324 |
282= 784 |
| 92= 81 |
192= 361 |
292= 841 |
| 102= 100 |
202= 400 |
302= 900 |
Patterns and Properties
- The Patterns in the Units Digit of Square Numbers: Square numbers exhibit intriguing patterns in the units digit, providing insights into their properties. By recognizing these patterns, we can quickly determine the units digit of a square number without calculating the entire square.
Examples:
- The units digit of a square number ending in 1 is always 1. For example, 1² = 1, 11² = 121, and 21² = 441.
- The units digit of a square number ending in 4 is always 6. For instance, 4² = 16, 14² = 196, and 24² = 576.
- The units digit of a square number ending in 5 is always 5. Examples include 5² = 25, 15² = 225, and 25² = 625.
- The units digit of a square number ending in 6 is always 6. For example, 6² = 36, 16² = 256, and 26² = 676.
- The units digit of a square number ending in 9 is always 1. Examples include 9² = 81, 19² = 361, and 29² = 841.
- The Relationship between the Square of an Even Number and the Square of its Half: The square of an even number is always four times the square of its half. For instance, (2 * n)² = 4 * (n²), where n represents any positive integer.
Example:
For example, the square of 8 (2 * 8 = 16) is 64, and the square of 4 (half of 8) is 16. Four times 16 equals 64.
- The Relationship between Consecutive Square Numbers: The difference between two consecutive square numbers is always equal to the sum of the two numbers.
Example:
The difference between 9 and 16 is 7, which is equal to 9 + 7. Similarly, the difference between 16 and 25 is 9, equal to 16 + 9.
Applications of Square Numbers
Square numbers find practical applications in various fields, providing a foundation for measurement, calculations, and problem-solving.
- Measurement of Areas: Square numbers play a crucial role in measuring the areas of squares and rectangles. The area of a square is calculated by squaring the length of its side. Similarly, the area of a rectangle can be determined by multiplying its length and width, which are often represented by square units.
- Calculating Distances in Coordinate Systems: The Pythagorean theorem, which involves square numbers, is instrumental in calculating distances in coordinate systems. When we have two points represented by their coordinates (x₁, y₁) and (x₂, y₂), the distance between them can be found using the formula √((x₂ - x₁)² + (y₂ - y₁)²).
- Understanding Quadratic Equations: Quadratic equations, which have a wide range of applications in mathematics, physics, and engineering. Quadratic equations involve terms with squares, such as ax² + bx + c = 0. Solving these equations often requires manipulating and analyzing square numbers.
- Mathematical Patterns and Sequences: Square numbers are fundamental elements in mathematical patterns and sequences, like the Fibonacci sequence and Pascal's triangle.
Conclusion
Square numbers provide a rich landscape for exploration and understanding in mathematics and beyond. From the intriguing patterns in their units digit to their relationships with even numbers and consecutive squares, square numbers offer fascinating insights into mathematical structures. Additionally, their practical applications in areas such as measurement, coordinate systems, and quadratic equations highlight their relevance in real-world scenarios. Embracing the world of square numbers unlocks a multitude of possibilities for problem-solving, measurement, and intellectual growth.
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now










