MatrixMatrix is very useful in engineering calculations. Several mathematical operations involving matrices are important. In this section, we will learn about the matrix, its notation, types, operations, and applications. What is the matrix?The matrix is a set of numbers that are arranged in horizontal and vertical lines of entries. The horizontal entries called rows, and the vertical entries called columns. The numbers are called the elements or entries of the matrix. It is written inside a pair of square brackets []. In other words, it is an array of numbers. It is a rectangular representation of numbers in the form of an array. Matrix NotationMatrix is usually denoted by a capital letter and its elements denoted by the small letters along with subscript of the row and column number. The row and column are denoted by the lower-case letter m and n, respectively. The size of the matrix is defined by the number of rows and columns that it contains. A matrix with m rows and n columns is called m × n matrix. It contains a total of m × n elements. For example: 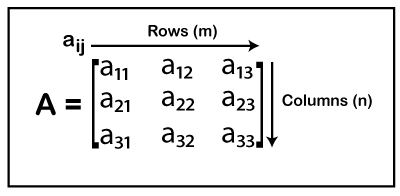
In the above matrix, aij (i represents row number, and j represents column number) are the elements of the matrix. There are three rows and three columns, so there is a total of nine elements in the matrix. The matrix may contain any number of rows and columns. For example: 
Types of MatricesThere are the following types of matrices: Empty Matrix: A Matrix with no rows and no columns is called an empty matrix. For example: [ ] Row Matrix: A matrix that has only a row is called a row matrix. It is also known as the row vector. For example: [4 3 6] Column Matrix: A matrix that has only a column is called a column matrix. It is also known as the column vector. For example: 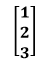
Zero Matrix: A matrix whose all elements are zero is called a zero matrix. It is also known as the null matrix. For example: 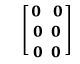
Square Matrix: A matrix in which row and column dimensions are equal (m=n) is called the square matrix. For example: 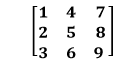
Diagonal Matrix: A square matrix in which all the non-diagonal elements are zero and contain at least one no-zero element in its principal diagonal is called the diagonal matrix. For example: 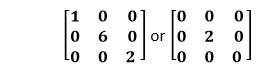
Scalar Matrix: A diagonal matrix whose all diagonal elements are equal is called the scalar matrix. The scalar matrix cannot be a unit matrix, while a unit matrix can be a scalar matrix. For example: 
Unit Matrix: A scalar matrix whose principal diagonal elements are one and all non-diagonal elements are zero is called the unit matrix. It is also called an identity matrix. It is denoted by the letter I. It is also a scalar matrix. 
For example: 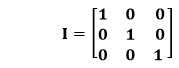
Triangular Matrix: It is a special kind of square matrix that forms a triangle either upper or lower to its principal diagonal. There are two types of the triangular matrix:
aij=0 for i<j
For example: 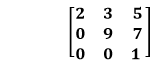
aij=0 for<ij
For example: 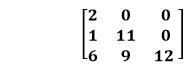
Submatrix: A submatrix of a matrix is determined by deleting any rows or columns or both. For example, consider the following matrix: 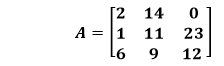
From the above matrix A, we can generate a submatrix. We are deleting the 2nd row and 3rd column. After deleting, we get the following submatrix: 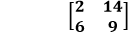
Applications of Matrices
Operations on MatrixWe can perform the following operations on the matrix:
Addition of MatricesThe sum om of two matrices can be done by adding the elements matching with the positions. Remember that both matrices must be of the same size. The resultant matrix is also of the same size.
(A+B)ij = Aij + Bij
Suppose, there are two matrices A and B, each of size 3×3. 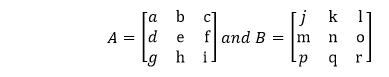
The sum of A + B will be: 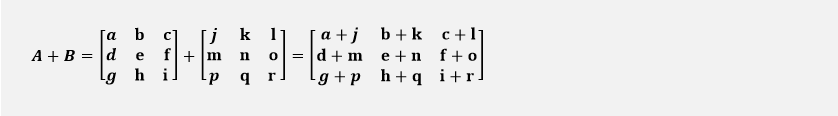
Properties of Addition
Example: Add the following matrices A and B. 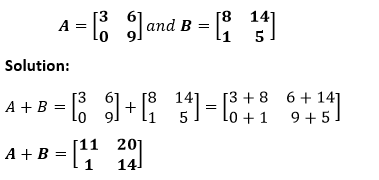
Subtraction of MatricesThe subtraction of two matrices can be done by subtracting the elements matching with the positions. In other words, it is an addition of a negative matrix. Remember that both matrices must be of the same size. The resultant matrix is also of the same size.
(A-B)ij = Aij - Bij
Suppose there are two matrices A and B, each of size 3×3. 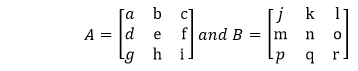
The subtraction of A - B will be: 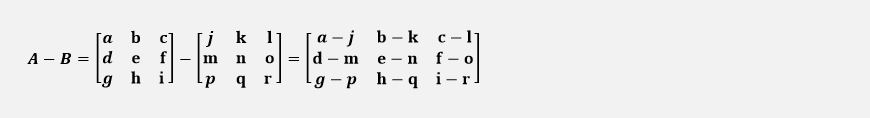
Example: Subtract the following matrices A and B. 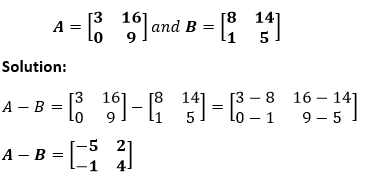
Multiplication of MatricesMatrix multiplication is the dot product of the rows and columns. The dot product is the sum of the products of the matching entries of the two sequences of the numbers.
First matrix's number of columns = Second matrix's number of rows
Properties of Multiplication
Example : Multiply the following matrices. 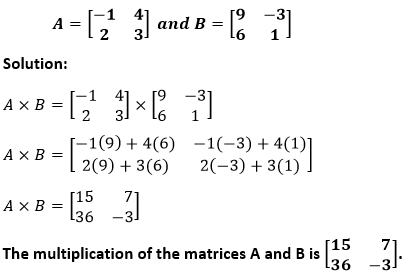
Division of MatricesThe division of the matrices is a tricky process. To divide the two matrices, we perform the following steps:
Suppose A and B are two matrices, then: 
Where B-1 represents the inverse of B. Example: Divide the following matrices A and B. 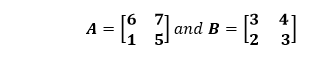
Solution: A is the numerator, and B is the denominator. First, we will find the inverse of B. 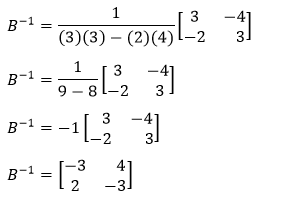
Now multiply the dividend matrix by the inverse. 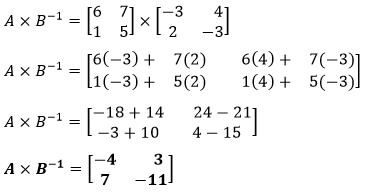
Scalar MultiplicationWhen a matrix is multiplied by a scalar (constant) is called scalar multiplication. In the scalar multiplication, we multiply each element of the matrix by the scalar. Suppose a matrix A of size 3×3 is given. 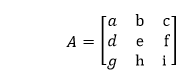
It is multiplied by a constant k then the scalar multiplication k × A will be: 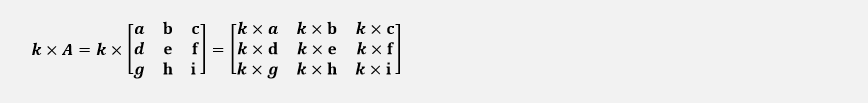
Properties of Scalar MultiplicationLet, A and B two matrices of size m × n, and a and b are two scalars. Then:

The inverse of a MatrixSuppose that we have a square matrix A, whose determinant is not equal to zero, then there exists an m×n matrix A-1 that is called the inverse of A such that: AA-1 = A-1A = I, where I is the identity matrix. It is easy to find the inverse of a 2×2 matrix in comparison to 3×3 or 4×4 matrix. Follow the steps to find the inverse of a 2×2 matrix.
For example, A is a 2×2 matrix. 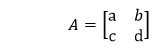
Its determinant is (ad-bc) that is not equal to zero, then the inverse of the matrix will be: 
There are three methods to find the inverse of the large matrix.
Properties of Inverse Matrix
Transpose MatrixWhen we convert the rows into columns and columns into rows and generates a new matrix with this conversion is called the transpose matrix. It is denoted by AT or A′, or Atr, or At. For example, consider the following matrix: 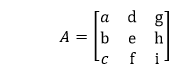
The transpose of the above matrix is: 
Properties of Transpose MatrixLet, A and B are two matrices and k is a real number, then:

Negative of a MatrixLet, A=aij be a m×n matrix. The negative of the matrix A is the m×n matrix B=bij such that bij=-aij for all i, j. The negative of the matrix A is written as -A. 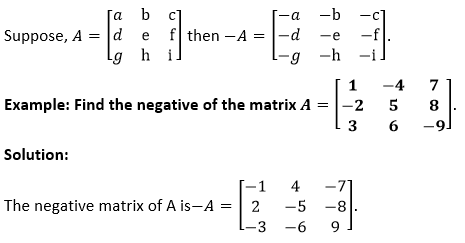
Next TopicMatrix Multiplication
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









