Cayley-Hamilton TheoremIn the wide field of mathematics, the Cayley-Hamilton Theorem has a brilliant and deep result that shows its usefulness in algebra and polynomial theory. This theorem is named after the discoverers of this theorem, "Arthur Cayley and William Rowan Hamilton," this theorem holds an important place in mathematics. It has various applications in various fields, including physics, engineering, and computer science. In this article, we will learn about the Cayley-Hamilton Theorem, its history, statement, proof, and applications, and end it with a conclusion. The Origin of Cayley-Hamilton TheoremThe Cayley-Hamilton Theorem finds its roots in the 19th century, a period that was marked by big mathematical discoveries and advancements and two famous mathematicians of that era, Arthur Cayley (born in 1821 and died in 1895) and William Rowan Hamilton (born in 1805 and died in 1865), played important roles in the development of this theorem. Arthur Cayley was a British mathematician famous for his groundbreaking work in the field of algebra and was particularly interested in the study of matrices and linear transformations. He made significant contributions to the field of linear algebra, and his exploration of the characteristics of matrices laid the foundation for the Cayley-Hamilton Theorem. On the other hand, William Rowan Hamilton was an Irish mathematician and physicist. He is best known for his work on quaternions and his contributions to the development of modern algebra. Although Hamilton is not as closely associated with the theorem as Cayley, his work on matrices and polynomials significantly influenced its formulation. The Cayley-Hamilton Theorem emerged as a joint effort between these two mathematicians, with Cayley initially formulating the theorem in the context of linear transformations and Hamilton later refining its statement in terms of matrices. Some PointsThe Cayley-Hamilton Theorem provides a powerful and surprising result regarding the behaviour of square matrices and their characteristic polynomials; in essence, it states that every square Matrix satisfies its characteristic equation. Before we get to learn about the Cayley-Hamilton Theorem, we have to get a better understanding of some terms, which are discussed below:
Definition of Cayley-Hamilton TheoremThe Cayley-Hamilton theorem states that a square matrix will satisfy its characteristic polynomial equation; the characteristic polynomial is related to the determinant of the given Matrix, and its eigenvalues are the roots of that polynomial. For a better understanding of this concept, let us consider a square matrix A with n rows and n columns; then the characteristic polynomial of the considered Matrix is obtained by taking the determinant of (λ * In - A); here, In is the Identity matrix of n order, λ is a scaler quantity. P(λ) = det (λ * In - A) P (A) = An + an-1 * An-1 + … + a1 * A + a0 * In = 0 Or P (A) = 0, where A is an n x n square matrix. 
The Cayley-Hamilton Theorem says that the characteristic polynomial equation of a complex or a real matrix is always equal to a zero matrix; the characteristic polynomial, i.e., p (λ) = det (λ * In - A), which can also be expressed as p (λ) = an * λn + an-1 * λn-1 + … + a1 * λ + a0 * λ0. We can say that this is a monic polynomial in which the leading coefficient, which is the coefficient of the highest degree variable, will always be equal to zero (1); this implies an = 1 here an-1, …, a1, a0 are coefficients of the variables λn-1, …, λ1, λ0 respectively. Example for showing Cayley-Hamilton TheoremLet us consider a square matrix A = As the characteristic equation is given by p (λ) = det (λ * In - A), so 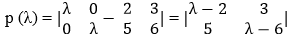
On opening determinant, we get: (λ - 2) * (λ - 6) - 15 λ2 - 6λ - 2λ + 12 -15 p (λ) = λ2 - 8λ - 3 Putting A in the place of λ in the above equation, we get: P (A) = A2 - 8A - 3In After putting the required values in the above equation and the required calculation, we will get the final value as zero (0), which we must show. Proof of Cayley-Hamilton TheoremIn mathematics, many methods can be used to provide proof of this theorem, but the easiest one is that we can use the substitution method. Let us consider a square matrix A = So, we have to prove p (A) = A2 - (e + h) * A + (eh - fg) * I2 = 0 L.H.S = A2 - (e + h) * A + (eh - fg) * I2 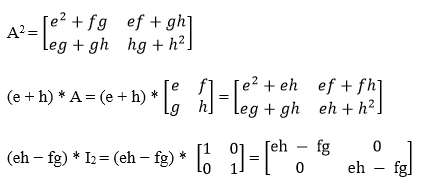
Putting all these values in L.H.S, we get: 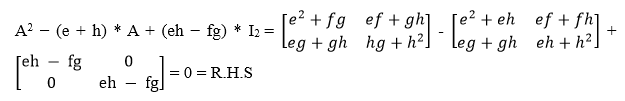
Similarly, we can do this proof for a higher-order square matrix. Applications of the Cayley-Hamilton TheoremThe Cayley-Hamilton Theorem has found its applications across various fields of mathematics and science; some of its notable applications are discussed below:
Frequently Asked QuestionedQ1: What do you understand by the Cayley-Hamilton theorem? Answer: The Cayley-Hamilton theorem is a fundamental result in linear algebra, stating that all square matrices satisfy their characteristic equation. This holds over a commutative ring, a real or complex field.
Q2: What is the formula for the Cayley-Hamilton Theorem? Answer: The formula for the Cayley-Hamilton theorem involves using a provided n × n matrix A, an n × n identity matrix I, and a variable x. Specifically, the distinctive polynomial of matrix A, denoted as p(x), is expressed as follows: p(x) = |x - A|
Q3: Is this theorem applicable to all types of matrices? Answer: The Cayley-Hamilton theorem is exclusively applicable to square matrices.
ConclusionThe Cayley-Hamilton Theorem was discovered from the collaboration of two mathematical giants, Arthur Cayley and William Rowan Hamilton, and stands as a profound and versatile result in linear algebra and polynomial theory; its importance lies in the fact that it reveals an inner connection between matrices and their characteristic polynomials, that allows us to manipulate matrices through their mathematical descriptors. Though complex, the proof of the theorem shows the beauty and hardness of mathematical reasoning; its applications extend far beyond pure mathematics, finding applications in fields as diverse as physics, engineering, computer science, and control theory. As we learn deeper into mathematics and its practical applications, the Cayley-Hamilton Theorem shines as a guiding light, showing the brilliance of those who contributed to the vast scope of mathematical knowledge.
Next TopicGreen's Theorem
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share




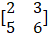 . We will prove the Cayley-Hamilton theorem for matrix A.
. We will prove the Cayley-Hamilton theorem for matrix A.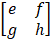 ; which is a 2 x 2 matrix, according to the Cayley-Hamilton Theorem p (A) = A2 - (e + h) * A + (eh - fg) * I2 = 0 (Zero Matrix)
; which is a 2 x 2 matrix, according to the Cayley-Hamilton Theorem p (A) = A2 - (e + h) * A + (eh - fg) * I2 = 0 (Zero Matrix)




