Square Root 1 to 25

In mathematics, one concepts that we learn early on is squaring a number (multiplication a number with itself). Square root is just inverse of square. Square root of any given number is the value, when multiplied with itself results in the original number. Square roots are crucial in mathematics. For instance, square root of 81 is 9, since 9 * 9 = 81. They are useful in solving equations, applying the Pythagorean theorem, measuring distances, calculating standard deviation, exploring complex numbers, etc. Square roots are essential tools for problem-solving.

Definition

Square root of any non-negative real number is a value that, when multiplied by itself, results in original number. We denote square root of a long non-negative real number "x," by the symbol "√x" or "x^(1/2)".

The square root symbol is "√" termed radical sign or radix, and the number whose square root is being calculated is called radicand. For instance, in √25 = 5, 25 is the radicand and 5 is square root of 25.

Basic Properties of Square Roots

Fundamental properties of square roots that we use extensively in mathematics and other related fields are:

• Non-negativity: Non-negative real number can never have negative square roots.
• Principal square root: Any positive real number "x," will have two square roots, one positive and other negative. The unique positive real number called the principal square root (√x).
• Square root of zero: Zero has only one square root, that is 0 (√0 = 0).
• Multiplicative property: For any two positive real numbers a,b √(ab) = √a * √b.
• Division property: For any two positive real numbers a,b √(a/b) = (√a) / (√b), where b ? 0.
• Rational numbers: Square root of a perfect square is always a rational number.
• Irrational numbers: Square root of a non-perfect square is an irrational number.
• Operations with square roots: Basic arithmetic operations can be performed with square roots.

Square Roots of Numbers 1 to 25:

Now let's learn the principal square roots of numbers from 1 to 25.

Methods of Calculating the Square Root

The square root of the rest of the numbers can be calculated by following three methods:

1) First method: Prime Factorization

It is the easiest and simple method of finding a square root. You can follow following steps to find square roots by prime factorization method.

1. Factorize the given number into prime factors.
2. Make pairs of same prime factors.
3. Pick out one prime factor from every pair.
4. Multiply one prime factor from each pair to get your answer

After multiplication, the product that came out is considered the square root of the required number.

For example, let's take a number 576 and find its square root with this method.

The prime factor of 576 should be:

= 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3

= 2 x 2 x 2 x 3

= 24

Therefore square root of 576 is 24.

2) Second Method: Long Division Method

The long division method is lengthy and slightly challenging to understand at once but suitable for finding the square root of large numbers. This method not only let us find square roots of perfect squares but also of non-perfect squares with high accuracy.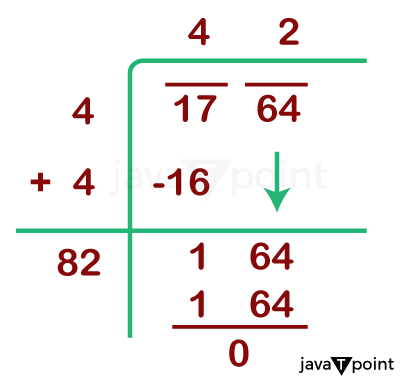

1. Start by pairing digits of the given number from the decimal point.
2. Find largest number "x" such that square of "x" is less than or equal to the first pair.
3. Subtract square of "x" from the first pair and bring down the second one.
4. Find largest number "y" such that "xy" when multiplied by "y" is less than new dividend.
5. Repeat above steps until all pairs have been brought down.
6. If the number is perfect square, you will get zero as the remainder and quotient will be your answer.
7. If the number is not a perfect square, then add decimal to quotient to bring down pair of zeros, and repeat step 1 to 4. Do this until you get answer with required accuracy or a repeating pattern occurs in quotient.

C) Third Method: Repeated Subtraction Method

You can calculate the square root of a number by subtracting successive odd number from a perfect square until you reach zero. The step at which you reach zero, will be your answer. Keep in mind that if the given number is not perfect square, you will not get zero at any step.

For example, lets us use this method to find the square root of 225.

The steps for repeated subtraction for number 225 are as follows:

1: 225 - 1 = 224

2: 224 - 3 = 221

3: 221 - 5 = 216

4: 216 - 7 = 209

5: 209 - 9 = 200

6: 200 - 11 = 189

7: 189 - 13 = 176

8: 176 - 15 = 161

9: 161 - 17 = 144

10: 144 - 19 = 125

11: 125 - 21 = 104

12: 104 - 23 = 81

13: 81 - 25 = 56

14: 56 - 27 = 29

15: 29 - 29 = 0

You can see that after repetitive subtraction of 225 from 1, we reach zero (0) in the fifteenth step. So we can conclude that 15 is the square root of 225 (√225= 15). We can verify this by finding the square root 225 from another method.

Applications and Examples:

Square roots find applications in diverse fields, including mathematics, physics, engineering, finance, and computer science. Some applications of square roots are:

1. Solving quadratic equations.
2. Calculating lengths in right triangles (Pythagorean theorem).
3. Finding magnitudes of complex numbers.
4. Determining vector magnitudes in physics.
5. Used in electrical circuits and signal processing.
6. Calculating investment returns and interest rates in finance.
7. Essential in computer science algorithms and cryptography.

Historical Perspective:

The square root is not a new concept as the ancient Indians, Chinese, Egyptians, and Greeks used it. The origin of "√" the root symbol has many stories. Many scholars assume that the square root originates from the letter 'r' and that the Latin word radix's first letter, r, stands for root. Another origin story of the square root symbol came from the Arabic letter ڄ which was placed in its original form ﺟ in the word جذر - root. One should remember that the Arabic language is written from right to left.

Initially, the square root symbol (√) was like this, which didn't include a horizontal "bar" over the number inside the square root or radical symbol. In Latin, the "bar" is called "vinculum," which means bond. Now, in the present time, the square root symbol with a bar (vinculum) is used every day. Albert Girard has suggested the notation of the higher degrees of a root (more than square root) where he put the degree index within the opening of the radical sign?for example, ³√ or ⁴√. The real meaning of the word radical is foundational, reaching the root cause but not far-reaching or extreme.

Conclusion:

Understanding square roots and being able to calculate them is crucial in both mathematics and daily life. Square roots have several applications in mathematics and other related subjects. Without the help of square roots we won't be able to understand complex numbers, or use Pythagoras theorem in right triangle, measure distances two points of Cartesian plan, or solve quadratic equations. Square roots are an essential tool that unlocks mysteries of numbers and enables us to explore the depths of mathematical concepts and practical problems alike.