What is 10% of 5000?

Percentage is an important concept in Mathematics and everyday life. It is used to express proportions and make comparisons. In this article, we will learn about percentages and explore the 10% of 5000 calculation. After understanding this basic concept, we will understand how the percentage work and apply this knowledge to various real-life applications.

Understanding Percentage

Before we learn the 10% of 5000 calculation, let's understand clearly "What is the percentage?" A percentage represents a fraction of the whole multiplied by a hundred (100); it helps us express parts of a whole in a standard way. Percentages are denoted by the symbol "%."

What is the Actual Meaning of 10% of 5000?

In particular, 10% of 5000 is 500.

We can understand this concept by simply assuming 5000 as 100 equal parts and objects and can assume anything; then 10 parts or objects from those 100 equal parts are considered 10%; for our case, 500 is the answer.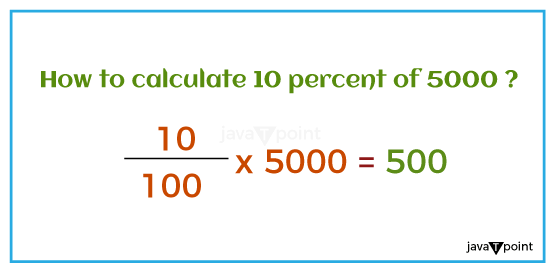

Steps to Calculate 10% of 5000

We will learn how to calculate 10% of 5000 with the help of simple steps explained in the following lines.

Step 1. First, write the product of both numbers, i.e., 10% and 5000, as shown below.

10% * 5000

Step 2. As we know, the meaning of percentage is the 100^th part of a number or anything, so that we can replace the "%" with (1 / 100).

10% * 5000 = (10 / 100) *5000

Step 3. Using the rules of multiplication and simplification, we get the following:

10% * 5000 = (10 / 100) *5000

50000 / 100

500

Real-World Applications

Understanding percentages and their calculations can be very helpful in various real-life situations. Let us discuss some examples:

• Sales and Discounts: Suppose you are shopping and get to know that a product has a 10% discount on the purchase. If the original price is $5000, you can calculate the discounted price by subtracting 10% of $5000 (or $500) from the original price, resulting in a final price of $4500.
• Tips and Thanksgiving: When dining at a restaurant, leaving a gratuity for the service is customary. If you wish to leave a 10% tip on a $5000 bill, you would calculate 10% of $5000 (or $500) and add it to the total bill, resulting in a final amount of $5500.
• Financial Investments: Investors often analyze percentages to make informed decisions. For example, if an investment has an annual return of 10%, you can calculate the return on a $5000 investment by multiplying $5000 by 10% to find the yearly return or profit of $500.

Some Solved Examples

Q. What is 5% of 1500?

Solution:

Step 1. 5% * 15

Step 2. 5% * 15 = (5 / 100) * 1500

Step 3. 5% * 15 = (5 / 100) * 1500 = 7500 / 100 = 75

Q. What is 21% of 5100?

Solution:

Step 1. 21% * 5100

Step 2. 21% * 5100 = (21 / 100) * 5100

Step 3. 21% * 5100 = (21 / 100) * 5100 = 1,07,100 / 100 = 1071

Q. What is 17% of 2000?

Solution:

Step 1. 17% * 2000

Step 2. 17% * 2000 = (17 / 100) * 2000

Step 3. 17% * 2000 = (17 / 100) * 2000 = 34,000 / 100 = 340

Q. What is 88% of 91?

Solution:

Step 1. 88% * 91

Step 2. 88% * 91 = (88 / 100) * 91

Step 3. 88% * 91 = (88 / 100) * 91 = 8008 / 100 = 80.08

Q. What is 39% of 5000?

Solution:

Step 1. 39% * 5000

Step 2. 39% * 5000 = (39 / 100) * 5000

Step 3. 39% * 5000 = (39 / 100) * 5000 = 1,95,000 / 100 = 1,950

Q. What is 20% of 5000?

Solution:

Step 1. 20% * 5000

Step 2. 20% * 5000 = (20 / 100) * 5000

Step 3. 20% * 5000 = (20 / 100) * 5000 = 1,00,000 / 100 = 1,000

Conclusion

Percentages are a fundamental concept of Mathematics that allows us to express proportions and make comparisons. In our case of calculating 10% of 5000, we multiply the total value by 10% (0.10) to obtain the result. This knowledge is useful in mathematics and applicable in various real-world scenarios, such as sales, gratuity, and financial investments. Understanding percentages and proportions can enhance our problem-solving abilities and help us make informed decisions in various aspects of life.