What is 10 to The Power Negative 4

Numbers in mathematics are not restricted to positive integers or whole numbers. There are also negative and fractional numbers, allowing us to explore a wide range of numerical possibilities. One fascinating notation is "10 to the power of negative 4." We will go into the meaning, relevance, and uses of this unusual mathematical notation in this article, providing a complete knowledge of its implications.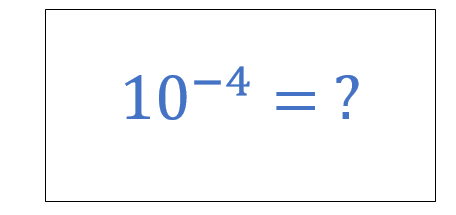

Understanding Exponentiation:

To realise the relevance of "10 to the power of negative 4," you must first understand the notion of exponentiation. Exponentiation is the process of multiplying a number (the base) by itself a certain number of times (the exponent). In the term "10 to the power of 2," or 102, for example, the base 10 is multiplied by itself twice, yielding 100. Similarly, "10 to the power of 3," or 103, signifies multiplying the base 10 by itself three times to get 1,000.

Defining Negative Exponents:

Negative exponents add an unusual twist to this notion by allowing fractional values or reciprocals to be represented. To demonstrate this, consider the expression "10 to the power of negative 4," or 10^-4. We divide 1 by 10 raised to the power of 4 instead than multiplying the base 10 by itself four times. In other terms, 10^-4 is equal to one divided by 10^4. This suggests that "10 to the power of negative 4" is a fraction with 1 as the numerator and 10,000 (10^4) as the denominator.

Decimal Notation and Negative Exponents:

One of the most practical applications of negative exponents is the representation of numbers in decimal notation. Consider the expression 10^-1, which signifies dividing 1 by 10 (10^1). This yields a decimal value of 0.1, demonstrating the relationship between negative exponents and the positioning of decimal points. Similarly, 10^-2 corresponds to 1 divided by 100 (10^2), resulting in the decimal value of 0.01. Extending this pattern, "10 to the power of negative 4" implies dividing 1 by 10,000 (10^4), giving us a decimal value of 0.0001.

Scientific Notation and Negative Exponents:

Scientific notation is a widely used format in science, engineering, and other fields to represent very large or very small numbers in a more compact and convenient manner. Negative exponents play a fundamental role in expressing numbers using scientific notation. For example, the speed of light, approximately 299,792,458 meters per second, can be expressed as 2.99792458 × 10^8 m/s. Here, the negative exponent 8 signifies that the decimal point moves eight places to the left, resulting in a smaller magnitude while preserving the value.

Applications of 10 to the Power of Negative 4:

Now that we have a solid understanding of "10 to the power of negative 4" and its broader implications, let's explore some practical applications where this notation finds relevance:

• Physical Sciences: When working with really tiny numbers in scientific study and analysis, the phrase "10 to the power of negative 4" is frequently used. It could, for example, in physics signify a minute amount of electric charge or the strength of a faint signal.
• Financial Calculations: In financial and investing settings, negative exponents are crucial. When represented as percentages, interest rates can be reduced to decimals by employing negative exponents. For instance, the decimal point is moved two spaces to the left in the expression for a 5% annual interest rate, which is written as 0.05 or 5*10^-2.
• Microbiology and Medicine: The expression "10 to the power of negative 4" can be used to describe the concentration of chemicals or bacteria in a sample in the fields of microbiology and medicine. It enables scientists and medical practitioners to measure and contrast the presence of tiny organisms in various environments, such as bacteria or viruses.
• Probability and Statistics: Applications of negative exponents can be found in statistics and probability. Uses of negative exponents in probability, especially when dealing with infrequent occurrences, helps us in expressing the possibility that such events will occur. For instance, 10^-4 can be used to describe the likelihood of winning a lottery with chances of 1 in 10,000.
• Electronics and Circuit Design: Negative exponents are integral to understanding the relationship between voltage and resistance in electrical circuits. Ohm's Law, which states that voltage (V) equals current (I) multiplied by resistance ®, can be expressed as V = I × 10^-4R. This notation highlights the relationship between resistance and the resulting voltage drop across a component.

Conclusion:

"10 to the power of negative 4" represents a unique mathematical expression that holds various applications and implications across different disciplines. Understanding the concept of negative exponents enables us to comprehend fractional values, decimal notations, and scientific notation, allowing for a more concise and convenient representation of numbers. Whether in the physical sciences, finance, microbiology, or electronics, this mathematical notation finds utility in quantifying small quantities, expressing probabilities, and facilitating calculations in numerous fields.