Binary formula

Binary is a number represented in the form of two digits, '0' and '1.' We can also define it as a number formed with digits 0 and 1. For example,

0110

It is a binary number equivalent to the decimal number 5. A binary number can be converted to a decimal number system, octal number system, and hexadecimal number system.

A binary number is represented with a base of 2. For example,

(11001110)₂

The digital transmission of signals is generally in the form of binary digits. The computer programming languages and their technology are all based on binary digits. The input provided to the computer is first converted to the understandable computer language (binary language). It is done with the help of an assigned ASCII code, which stands for American Standard Code for Information Interexchange. The information is a further process and is presented to the user as the output after converting the binary language to the user language.

Here, we will discuss the following:

Addition of binary numbers

Subtraction of binary numbers

Multiplication of binary numbers

Binary to Decimal

Binary to Octal

Binary to Hexadecimal

Let's start.

Addition of binary numbers

The addition is slightly different from the normal addition but quite simple. It is due to the addition using two numbers, 0 and 1. We can easily add two or more two binary digits.

For example,

1 + 1 = 10

0 as the result and 1 as the carry

11 + 01 = 100

The addition of three one's can be calculated as:

1 + 1 + 1 = (1 + 1) + 1

= 10 + 1

= 11

In a similar way, binary digits are added. Let's discuss some examples of adding binary digits.

Example 1:

Add binary numbers 110011 and 100111.

The addition process of binary numbers is similar to that of normal mathematical addition of numbers from 0 to 9. The only difference is the use of digits. Here, the process of addition is only in the form of two digits 0 and 1.

Step 1: Start from the right end.

Step 2: Add the numbers. For better understanding, we have listed the addition with the carry and final result in the below table:

We have listed the binary digits starting from the right end to the left end because addition always begins from the right end. We can consider any binary number as A or B from the given two numbers.

The final sum is 1011010.

Here, the number represented above the two given binary numbers is the carry. It is added along with the two digits of the two binary numbers.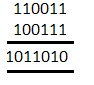

Verification

Let's verify the numbers after converting them to decimal.

Binary number 'A' in decimal = 51

Binary number 'B' in decimal = 39

Sum in decimal = 90

51 + 39 = 90

Hence, verified.

Example 2:

Add binary numbers 10110011 and 11100011.

Solution: The steps are listed below:

Step 1: Arrange the binary numbers one below the other.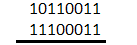

Step 2: Start the addition from the right end.

Here, the number represented above the two given binary numbers is the carry. It is added along with the two digits of the two binary numbers.

Or

Thus, the sum of two binary numbers 10110011 and 11100011 is 110010110.

Verification

Let's verify the numbers after converting them to decimal.

Binary number 'A' in decimal = 179

Binary number 'B' in decimal = 227

Sum in decimal = 406

179 + 227 = 406

Hence, verified.

Subtraction of binary numbers

We can easily subtract two binary digits.

There is no carry in subtraction. But, borrow is required when the subtraction is with the smaller number (0 - 1). Borrow is taken from the high order digit or 1. Let's discuss some examples for better understanding.

For example,

11 - 10 = 01

100 - 011 = 001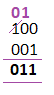

Here, the cut on a number represents borrow, which can be taken only from the binary digit '1'. If the adjacent digit is 0, borrow is taken from the next binary digit '1'. After borrow, the binary digit '1' becomes equal to 0. The succeeding digit that borrows 1 becomes equal to 1.

Since, the digit adjacent to the first digit from right end is 0, borrow is taken from the next digit as 1.

Thus, the borrowing process is similar to the borrowing process in mathematics, when a larger number is subtracted from the smaller number.

Let's discuss two examples for better understanding.

Example 1:

Subtract 1100110 and 0101110.

The steps are listed below:

Step 1: Arrange the binary numbers one below the other.

Step 2: Start the subtraction from the right end, as shown below.

We have listed the binary digits starting from the right to the left because subtraction always begins from the right end. The smaller is always subtracted from the larger number in a binary system.

Borrow - 0: Since, 0 (digit in number A) does not have its own value; it will further borrow 1 from the succeeding binary digit.

Borrow (1) - 0 = 1

The binary digit 1 after giving becomes 0.

Thus, the difference is 0111000.

Or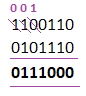

Thus, the difference between the two binary numbers 1100110 and 0101110 is 0111000.

Verification

Let's verify the numbers after converting them to decimal.

Binary number 'A' in decimal = 102

Binary number 'B' in decimal = 46

Difference in decimal = 56

102 - 46 = 56

Hence, verified.

Example 2:

Subtract 11011011 and 01110001.

The steps are listed below:

Step 1: Arrange the binary numbers one below the other.

Step 2: Start the subtraction from the right end, as shown below: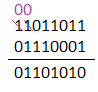

The subtraction of the given two binary numbers starts with each column one by one from the right end.

We know that,

0 - 1 = 1 with borrow 1

The third last column borrows 1 from the first digit of the second last column. It becomes 0 after giving 1 and again borrows from the last column.

In the last column,

0 - 0 = 0

Thus, the subtraction of the last column is 0.

Thus, the difference between the two binary numbers 11011011 and 01110001 is 01101010.

Verification

Let's verify the numbers after converting them to decimal.

Binary number 'A' in decimal = 219

Binary number 'B' in decimal = 113

Difference in decimal = 106

219 - 113 = 106

Hence, verified.

Multiplication of binary numbers

The multiplication of binary number is similar to the multiplication, but using only two digits 0 and 1. It follows the concept that a number multiplied by zero is always a zero.

Examples

Example 1:

Multiply 1001 and 011

Solution: We will perform the multiplication in a similar way as listed in the above table.

Step 1: Start the multiplication from right end.

Step 2: We will multiply each digit of the second number (011) with the first number (1001).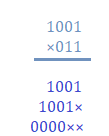

Step 3: Add the result after multiplication.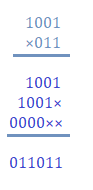

Verification

Let's verify the above multiplication after converting to decimal.

(1001)₂ = 9

(011)₂ = 3

The multiplication result of the two binary numbers is:

(011011)₂ = 27

Thus,

9 × 3 = 27

Hence, verified.

Binary to decimal

It is a number that is commonly used in day-to-day life. It has a base of 10. A decimal number is represented in the form of digits from 0 to 9, while a binary number is represented only in two digits, i.e., 0 and 1.

For example,

(X)₁₀

Where,

X is a decimal number

A binary number 'abcde' can be converted to the decimal number by multiplying every digit of a binary number with the powers of 2 starting from 0. The multiplication begins from the right end of the given binary number.

(e × 2⁰ + d × 2¹ + c × 2² + d × 2³ + e × 2⁴) and so on if a number is of greater count.

For example,

Example 1:

Convert binary number 10011 to decimal.

Solution: Let's consider a five digit binary number as abcde.

By comparing, we get:

a = 1, b = 0, c = 0, d = 1, and e = 1

(1 × 2⁰ + 1 × 2¹ + 0 × 2² + 0 × 2³ + 1 × 2⁴)

= (1 × 1 + 1 × 2 + 0 × 4 + 0 × 8 + 1 × 16)

= 1 + 2 + 0 + 0 + 16

= 19

The above conversion process is also shown in the below image: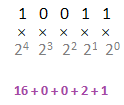

Example 2:

Convert the binary number 10011001 to decimal.

Solution: We will perform the similar process for conversion. We need to start the multiplication of the binary digits from the left end with the power of 2.

(1 × 2⁰ + 0 × 2¹ + 0 × 2² + 1 × 2³ + 1 × 2⁴ + 0 × 2⁵ + 0 × 2⁶ + 1 × 2⁷)

= (1 × 1 + 0 × 2 + 0 × 4 + 1 × 8 + 1 × 16 + 0 × 32 + 0 × 64 + 1 × 128)

= (1 + 0 + 0 + 8 + 16 + 0 + 0 + 128)

= 153

(10011001)₂ = (153)₁₀

Thus, the binary number 10011001 is equal to the decimal number 153.

A quick conversion of a few binary numbers is listed in the below table:

Binary to octal

Octal is a number represented as a base of 8 with numbers ranging from 0 to 7 (0, 1, 2, 3, 4, 5, 6, and 7). It is represented in the form of three bits. The conversion of octal numbers from 0 to 7 is the same as in decimal. In early ages, the octal number system was used as a computer programming language.

The conversion of octal numbers (0 - 7) to binary is listed in the below table:

After, 7 the number begins from 10 to 17, 20 to 27, 30 to 37, etc. It does not show the conversion of decimal digits 8 and 9. Hence, it is named an octal number system due to the involvement of only 8 digits from 0 to 7.

The conversion of octal numbers (10 - 17) to binary is listed in the below table:

It is the same three bits with prefix of '1.' Similarly, the conversion of 20 to 27 is also the same three bits with the prefix of '10' and '11' as the prefix for the conversion from 30 to 37.

There are two different methods to convert binary to octal.

1. Binary to octal
2. Binary to decimal to octal

Binary to octal

It is a direct conversion process from binary to octal, an easy and quick method. Examples

Example 1:

Convert 11001001 to octal

Step 1: Divide the given binary number into a pair of three digits starting from the right end.

11-001-001

Step 2: From the table, convert the binary number of three digits into octal.

(001)₂ = (1)₈

(11)₂ = (3)₈

Step 3: Combine the hexadecimal conversion digits.

11-001-001 = 3 - 1 - 1

= 311

Thus, the binary number 11001001 in the octal system is 311.

Example 2:

Convert 100100111001 to octal

We will first divide the given binary number into a pair of three digits starting from the right end and substitute the value of the octal number in it.

100-100-111-001

4 - 4 - 7 - 1

= 4471

Thus, the binary number 100100111001 in the octal system is 4471.

Binary to decimal to octal

It is a long process due to the conversion from binary to decimal and again from decimal to octal.

Example: 1

Convert binary number 10010 to octal.

Step 1: Binary to decimal

It can be converted to the decimal number by multiplying every digit of a binary number with the powers of 2 starting from 0. The multiplication begins from the right end of the given binary number.

(0 × 2⁰ + 1 × 2¹ + 0 × 2² + 0 × 2³ + 1 × 2⁴)

= (0 × 1 + 1 × 2 + 0 × 4 + 0 × 8 + 1 × 16)

= 0 + 2 + 0 + 0 + 16

= 18

Step 2: Decimal to octal

For this, we will divide the number by 8.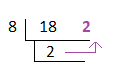

8 × 2 = 16 (remainder 2)

The right side shows the remainder. The octal value will be the remainder at the last at ten's place and remainder at the beginning at one's place. It means the octal conversion will be the order of the reverse remainders.

Thus, the binary number 10010 in the octal system is 22.

Binary to hexadecimal

The hexadecimal refers to sixteen (16) with a base of also 16. The numbers range from 0 to 9 and from A to F. The total range of hexadecimal is from 0 to 16, where numbers 10 to 15 are labeled as A to F. A hexadecimal digit is represented in the form of four digits.

The conversion of hexadecimal numbers from 0 to 9 is the same as in decimal.

The conversion of hexadecimal numbers (0 - 9) to binary is listed in the below table:

From 10 to 15, the numbers are listed as:

There are two different methods to convert binary to hexadecimal.

1. Binary to hexadecimal
2. Binary to decimal to hexadecimal

Binary to hexadecimal

It is the direct conversion process from binary to hexadecimal, which is also easy and a quick.

Examples

Example 1:

Convert 11001001 to hexadecimal

Step 1: Divide the given binary number into a pair of four digits starting from the right end.

1100-1001

Step 2: From the table, compare the binary digits with the hexadecimal number and substitute its value.

(1001)₂ = (9)₁₆

(1100)₂ = (C)₁₆

Step 3: Combine the hexadecimal conversion digits.

1100-1001 = C - 9

= C9

Thus, the binary number 11001001 in the hexadecimal system is C9.

Example 2:

Convert 100111 to hexadecimal

Step 1: Divide the given binary number into a pair of four digits starting from the right end.

10-0111

Step 2: From the table, compare the binary digits with the hexadecimal number and substitute its value.

(0111)₂ = (7)₁₆

(10)₂ = (2)₁₆

Step 3: Combine the octal conversion digits.

10-0111 = 2 - 7

= 27

Thus, the binary number 100111 in the hexadecimal system is 27.

Binary to decimal to hexadecimal

First, we need to convert the binary number to a decimal number and further it to hexadecimal.

Let's consider an example.

Convert 11011100 to hexadecimal.

Step 1: Binary to decimal

It can be converted to the decimal number by multiplying every digit of a binary number with the powers of 2 starting from 0. The multiplication begins from the right end of the given binary number.

(0 × 2⁰ + 0 × 2¹ + 1 × 2² + 1 × 2³ + 1 × 2⁴ + 0 × 2⁵ + 1 × 2⁶ + 1 × 2⁷)

= (0 × 1 + 0 × 2 + 1 × 4 + 1 × 8 + 1 × 16 + 0 × 32 + 1 × 64 + 1 × 128)

= (0 + 0 + 4 + 8 + 16 + 0 + 64 + 128)

= 220

(11011100)₂ = (220)₁₀

Thus, the binary number 11011100 is equal to the decimal number 220.

Step 2: Decimal to hexadecimal

For this, we will divide the number by 16.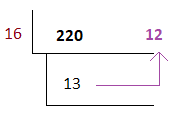

16 × 13 = 208 (remainder 12)

The right side shows the remainder. The hexadecimal conversion will be the order of the reverse remainders. It means that the first remainder comes at the last, and the last remainder comes at the beginning forming a hexadecimal number.

We know that 12 is equal to C and 13 is equal to D. Thus, the hexadecimal number is DC.

Thus, the binary number 11011100 in the hexadecimal system is DC.

(11011100)₂ = (DC)₁₆