Difference Between Relation and Function

In mathematics, Relation and Function are two fundamental concepts we usually encounter while studying. These concepts serve as the base for various mathematical theories and have applications across diverse fields, from calculus and algebra to computer science, and also in solving real-life problems. Both concepts are closely related, and one who has not fully understood them may think they are similar. However, these concepts have distinct characteristics and play different roles in understanding mathematics. So, in this article, we will get to know the concepts of Relation and Function, their definitions, properties, types, and differences, and conclude this article with a conclusion.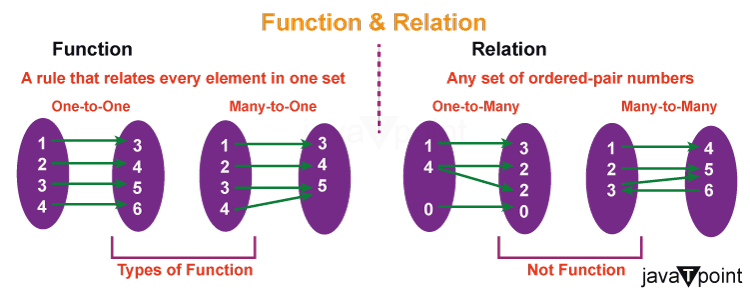

Definition of Relation

A Relation can be defined as the connection between two sets by any definition or means. In mathematics, it can also be defined as the collections of ordered pairs with one element from one set and another element from another set; so, a relation is a collection of ordered pairs containing entries from two sets respected to its elements.

For a better understanding, let us consider two sets named A and B, and we can take any element from these two sets; consider two elements from these sets as element "e" from A and "f" from B. Then the relation "R" between sets A and B is said to be a relation if order pair (e, f) are in relation. A and B are two arbitrary sets, all the ordered pairs of (e, f), where "e" is an arbitrary element from A and "f" is an arbitrary element from B, is called the Cartesian product of A and B.

We can also write this Relation as R: - A x B, defining it as A ? B = {(e, f)} I e ∈ A and f ∈ B} and keep in mind that A ? B ≠ B ? A. The Cartesian product is the concept that deals with ordered pairs, so the order in which the sets are considered is important. We use n(X) for the number of elements in a set X, and we have a formula to determine the number of elements in a relation: n (A ? B) = n(A) ? n(B).

Properties of Relations

Relations can show various properties, each contributing to their distinct characteristics, which are discussed below:

1. Reflexivity: A relation is called reflexive if every element in Set A is related to itself; in other words, for all 'a' in Set A, the ordered pair (a, a) belongs to the relation.
2. Symmetry: A relation is called symmetric if, for every pair (a, b) in the relation, the pair (b, a) is also present; in this case, if 'a' is related to 'b,' then 'b' is related to 'a'.
3. Transitivity: A relation is transitive if, whenever elements' a' and 'b' are related, and 'b' and 'c' are related, then 'a' and 'c' are also related; in other words, if (a, b) and (b, c) belong to the relation, then (a, c) must also belong to the relation.
4. Anti-Symmetry: A relation is anti-symmetric if whenever (a, b) and (b, a) are both in the relation, it implies that 'a' equals 'b'; in other words, if 'a' is related to 'b' and 'b' is related to 'a', then 'a' must be equal to 'b.'

Definition of Function

While relations show various mathematical concepts, functions provide a more specific and structured way to connect elements of sets. A function is a relation with the additional property that each element from Set A is associated with exactly one element from Set B.

In other words, the relation that shows the set of input elements to the set of particular outputs is called a Function. However, remember that each input in set A has a particularly single output element in set B in a defined function. A function is usually represented by "F or f."

F: - A ⟶ B

Two conditions must be satisfied to be a function:

1. Every a in A must be related to b in B, i.e., the domain of f must be X, not a subset of X.
2. There must be a uniqueness that can be expressed as:

If (a, b) is in F and (a, c) is in F

It is possible if and only if b = c.

Note: All functions are relations, but not all relations are functions.

Properties of Functions

Functions have distinct properties that differentiate them from general relations, which are discussed below:

1. Domain and Codomain: The set of all inputs for which the function is defined is called the domain (related to Set A), and the set of possible outputs, where the values of the function lie, is known as the codomain (related to Set B).
2. Unique Mapping: One of the important characteristics of a function is that each element in the domain (Set A) is mapped (shows output) to exactly one element in the codomain (Set B); this implies there are no duplicate outputs in the mapping.
3. Range: The range of a function is the set of all actual outputs obtained by applying the function to elements of the domain, and it is represented by the subset of the codomain that the function covers.

Types of Functions

Functions can have various types and classifications based on their properties; there are mainly three types of a function:

1. Injective Function or One-to-One Function: A function is called an injective function if each element in the domain maps to a distinct (unique) element in the codomain; this implies that no two different inputs have the same output.
2. Surjective Function or Onto Function: A function is called a surjective function if every element in the codomain has at least one pre-image in the domain; in other words, the function "covers" the entire codomain.
3. Bijective Function or One-One Function: A function is called a bijective function if it is both injective and surjective, so it establishes a one-to-one correspondence between the domain and codomain, meaning each element in the domain maps to a unique element in the codomain and its opposite is also true.

Difference in Terms of Mathematics

In mathematics, it is common to get confused with the terms "function" and "relation" for those unfamiliar with these concepts. While they may seem similar, it is very important to understand their differences to apply these concepts correctly. In particular, we can say that all functions are relations, but not all relations are functions.

A relation is a set of ordered pairs of elements that can be a subset of the Cartesian product, and it is a way of modeling ideas such as "greater than, equal to, and divides." A relation can have several outputs for a single input, which means it can exhibit item properties and convey meaning.

On the other hand, a function is a particular type of relation with only one output for each input. It is represented as an ordered triple set containing X, Y, and F, where X is the domain or input set, Y is the codomain or output set, and F is the set of ordered pairs in both "a and b." Each ordered pair contains a primary element from the "A" set, and the second element comes from the codomain, which satisfies the necessary condition; set B refers to the image of the function.

It is important to note that the domain and codomain are sets of real numbers, but the range does not have to be the entire codomain. While relations and functions connect items, their main distinction lies in their outputs; i.e. Functions have a unique output for each input, while relations can have multiple outputs for a single input. By understanding the differences between the two, we can apply them correctly and accurately to understand mathematical concepts better.

Conclusion

We can say that relations and functions have the same concept, i.e., they show how two different sets can interact. They are different in structure and purposes, i.e., Relations provide a wide network framework, allowing for multiple outputs. At the same time, functions offer a structured and unique mapping that is particularly useful for modeling and problem-solving. Understanding these two concepts' differences is important for building a solid foundation in mathematics and its applications across various fields.