Difference Between Permutation and Combination

In the wide field of Mathematics, Permutation, and Combination are two basic concepts that show various disciplines of mathematics, from probability theory and statistics to combinatorics and algebra. Their combinatorial nature interconnects both these concepts (Permutation and Combination) and has different characteristics and applications. So, in this article, we will learn about the concept of Permutation and Combination, definitions, properties, applications, and differences, and end this article with a conclusion.

Definition of Permutation

A permutation is a mathematical concept that deals with the arrangement of objects in a special order; in other words, a Permutation of a set of objects refers to an arrangement of those objects in a distinct order.

For example, consider a set of elements {A, B, C}.

The permutations of this set would be ABC, ACB, BAC, BCA, CAB, and CBA. In Permutations, the order of arrangement is important; if we alter the order of the results, it is a different permutation.

In terms of mathematics, if we have an 'n' number of different objects and we want to arrange them in 'r' positions, then the number of permutations is denoted by "ⁿP_r or n P r." It is calculated by the formula: n P r = n! / (n - r)!.

Where 'n!' read as n factorial, is the product of all positive integers from 1 to 'n,' and (n - r)! represents the factorial of the difference between 'n and r.' This formula ensures that the arrangement is distinct (without repetition) and ordered. We can also write n! = n (n-1) (n-2) … 1 and (n - r)! = (n - r - 1) (n - r - 2) (n - r - 3) … 1.

Types of Permutation

There are two types of Permutation based on the arrival of objects, which are:

1. With Repetition
2. Without Repetition

Let's discuss these types one by one.

1. Permutations with Repetition

We can understand this with the help of an example. Consider we have six (6) objects, and we have to select these objects, so in "How ways can we select these six (6) objects (with repetition)?"

We can solve this with 6⁶ = 6 x 6 x 6 x 6 x 6 x 6 = 46,656. So, we can select 6 objects in 46,656 ways with repetition. We can also understand this as 1^st object can be selected in 6 ways, 2^nd object can be selected in 6 ways, 3^rd object can be selected in 6 ways, 4^th object can be selected in 6 ways, 5^th object can be selected in 6 ways, 6^th object can be selected in 6 ways, this happened because repetition is allowed. So, we have this formula: 6! = 46,656 ways. So, the general formula becomes nⁿ.

2. Permutations without Repetition

In this Permutation, we will use the general formula to solve these types of problems in which repetition is not allowed. We will use the above example to put this in use, as we had six objects, and we had to select these objects one by one (but without repetition). So, we will put n = 6 and r = 6 in the above-described formula; we have 6 P 6 = 6! / (6 - 6)! = 6! = 720 ways.

Note: We have to remember that 0! = 1.

Permutations find many applications, such as solving probability problems involving arrangements, cryptography, organizing events, and generating passwords. For example, when selecting a president, vice president, and secretary from 10 candidates, the number of permutations can be calculated to determine the possible officer arrangements.

Definition of Combination

Combination, on the other hand, deals with the selection of objects from a set without considering the order of arrangement; in contrast to permutations, where ABC is distinct from BAC, these arrangements are similar in the concept of combinations since they contain the same elements. A combination represents the selection of 'r' objects from a set of 'n' without regard to the order of selection. Mathematically, the number of combinations denoted as "n C r or ⁿC_r" is given by the formula: n C r = n! / r! ⋅ (n-r)!

The denominator consists of the product of 'r!' and '(n - r)!', showing that the overcounting of equivalent combinations is not included. Combinations find applications in probability calculations involving the selection of items and in various fields like genetics, where the combination of alleles leads to genetic diversity. For instance, when forming a committee by selecting 3 members from a group of 10, you would use combinations to determine the number of different committee compositions.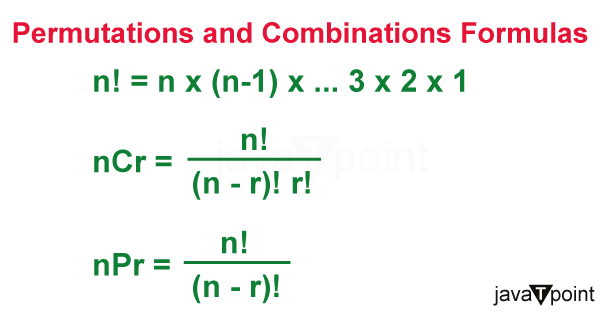

Key Differences

We will discuss the differences between Permutations and Combinations in this paragraph:

When to Use Which

• Permutations: If you have 5 books and want to arrange them on a shelf. Since the order matters, you would use permutations. There are 5 books for the first position, 4 for the second, 3 for the third, and so on. Therefore, the total number of permutations is 5 P 5 = 120.
• Combinations: Suppose you are at an ice cream shop with 8 different flavors, and you want to order 3 scoops of ice cream. Since the order of scoops doesn't matter, you would use combinations. The number of ways to choose 3 scoops out of 8 is 8 C 3 = 56.

Relation Between Permutation and Combination

We will use formulas of Permutation and Combination and establish a relation between these two concepts.

As, n P r = n! / (n - r)!

Multiply and divide by 'r!' in the numerator and denominator on the right-hand side.

We get n P r = r!. n! / r!. (n - r)!

As we know, n C r = n! / r!. (n - r)!

This implies n P r = (r!). n C r

So, we have a proper relationship between Permutation and Combination.

Applications of Permutation and Combinations

There are so many applications of these concepts in various fields other than mathematics; some of them are discussed below description:

1. Probability and Statistics: Permutations and combinations are used to calculate probabilities in various situations, such as drawing cards from a deck, rolling dice, or selecting objects from a set. Combinations are usually used in calculating the number of possible outcomes in a sample space, which is important for understanding and analyzing random events.
2. Sports and Tournaments: Permutations and combinations are important in organizing tournaments, scheduling matches, and determining the outcomes of competitions, such as in round-robin tournaments and knockout brackets.
3. Social Sciences and Marketing: In social sciences and marketing, the concepts of Permutation and combination are used to study patterns and behaviors, such as consumer choices, market segmentation, and voting systems.
4. Game Theory: The concepts of Permutation and combination are used to analyze game theory scenarios where players choose to optimize their outcomes. Combinatorial analysis helps determine the number of possible strategies, outcomes, and payoffs in different game situations.
5. Cryptography: Permutations and combinations play a role in cryptographic algorithms; for example, we can consider the example of generating encryption keys or ensuring the security of digital signatures so the arrangement of elements can have a particular impact on the strength (in terms of breach of the system) of the cryptographic scheme.

Conclusion

Permutations and combinations are interconnected by their combinatorial nature, and this serves distinct purposes in the field of mathematics and its applications in various fields. Permutations deal with the arrangement of objects in a specific order, while combinations focus on the selection of objects without consideration for order. These concepts' formulas, properties, and applications are different, making them invaluable tools for solving various problems across various disciplines. Understanding the difference between permutations and combinations helps solve mathematical and scientific real-life problems.