Difference Between Parabola and Hyperbola

In the field of Mathematics, a certain number of curves hold unique concepts that fascinate mathematicians due to their captivating properties and complex forms. Parabolas and Hyperbolas are two basic conic sections that show distinct characteristics, although they may appear similar to one who has not studied them. So, in this article, we will learn about the concepts of Parabolas and Hyperbolas, their differences, and real-life applications, ending this article with a conclusion.

Parabola

A Parabola is a U-shaped curve that can be created by intersecting a cone with a plane that is parallel to the side of the cone; this conic section has a notable property, which is that all the points on the Parabola are equidistance from a particular point called the focus and a straight line known as directrix. This geometric shape is quite similar to the concept of a convex mirror in Physics (not entirely): any parallel rays that strike the surface of a parabola are reflected so that they all converge at the focus point.

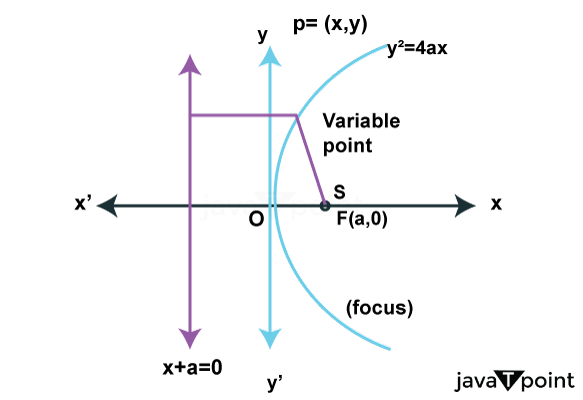
This particular shape of the Parabola finds its applications in various fields; in Physics, the trajectory of a projectile, for example, when we throw a ball in the air, follows a parabolic path under the application of gravity. This concept helps in applied physics, like building weapons like ballistics missiles and engineering; moreover, parabolic reflections are used in satellite dishes, telescopes, and headlights of vehicles, as they are used to gather or focus incoming signals or light rays.

Hyperbola

Unlike the Parabola, a Hyperbola comes into existence when a plane divides a cone parallel to its axis; the important feature of a hyperbola lies in the relationship between the distance from any point on the curve to two fixed focal points that are also known as foci, and that difference in distances remains constant for all points on the Hyperbola. On appearing, the Hyperbola presents two distinct branches that open away from each other, showing a mirror image of the conic section's symmetrical structure. This geometric shape is quite similar to the concept of a concave lens in Physics (not entirely).

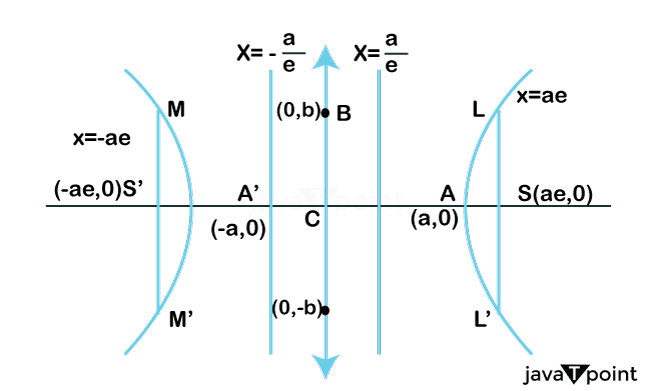
This particular shape of Parabola finds its applications not only in Mathematics but also in various scientific and practical fields, like in astronomy, the orbits of a comet and other celestial bodies are usually approximately estimated by hyperbolic trajectories; moreover, hyperbolic lenses are used in optics and photography to provide a unique way of capturing clear views or to correct certain lens distortion in the eye.

Differences

At first glance, one unfamiliar with Parabola and Hyperbola may think these shapes are similar. But both the shapes are quite different from one another; in this paragraph, we will discuss these differences:

1. Foci and Directrices: In a parabola, there is only one focus and a directrix for that focus; this parabolic shape ensures that any parallel rays that strike the surface of a parabola are reflected in such a way that they all converge at the focus point. On the other hand, Hyperbolas have two focal points (foci) and two directrices with respect to their foci; the distance relationship between these foci and the points on the Hyperbola defines the conic section.
2. Eccentricity: This concept of eccentricity plays an important role in understanding the difference between a parabola, Hyperbola, ellipse, and circle. The eccentricity of a conic section is a measure of how its shape is derived from that of a circle, denoted by "e." For a parabola, the eccentricity value equals one (1), which shows that it is unique from other conic sections. On the other hand, a Hyperbola has a value of eccentricity greater than 1, which shows that its shape is elongated and open in nature.
3. Shape Variability: Parabolas, apart from their size, have a consistent shape; this means that whether a parabola is enlarged or reduced in size, its curvature remains unchanged. Hyperbolas, on the other hand, are more diverse in shape; they can vary in their curvature and size, which results in hyperbolas that may appear narrower or wider.
4. Arms Orientation: In a Parabola, the arms of a parabola are parallel; two branches of a parabola are parallel to each other, with one side curving upward and the other downward. On the other hand, Hyperbola has non-parallel arms; the branches of a hyperbola open away from each other and curve in different directions.
5. Asymptotes: In mathematics, an asymptote is a line that a curve approaches as that curve is drawn or extends toward infinity. Parabola has no asymptotes, which is a notable difference from Hyperbola. Hyperbola, on the other hand, has two asymptotes showing the behavior of Hyperbola branches as they approach infinity.

Real-Life Applications

Understanding the differences between parabolas and hyperbolas not only increases our knowledge of mathematics but also has real-world implications. The concept and principles of conic sections find their application in various fields, which are discussed below:

Parabola

1. Satellite Dishes: The shapes of a satellite dish are quite similar to that of a Parabola, and the reason behind this is that shape allows the incoming signals to be focused at a single point, which is where the receiver is located (at the focus of the Parabola).
2. Projectile Motion: The trajectory of a projectile; for example, if we throw a ball or launch a rocket in the sky, they both follow a parabolic path. This property is used in fields like physics and engineering when we predict the motion of an object during freefall.
3. Optics: The mirrors of shapes like parabolas are used in telescopes, spotlights, and reflector antennas. The shape of the mirror allows it to focus incoming parallel rays of light to a single point, known as the focal point.
4. Construction: The shape of suspension bridges is usually similar to that of a parabola, and the reason behind this is that shape helps distribute weight and forces evenly, which makes the structure of the bridge more stable.
5. Automobile Headlights: Parabolic reflections are used in the headlights of automobiles to focus the light from a bulb into a beam that shines the road ahead of an automobile.
6. Solar Cooker: Solar cookers are usually made with curved mirrors that have the shape of a parabola to concentrate the sunlight into a single point (focus), where the cooking vessel is placed; due to this concept, the intensity of heat increases at a single point and the food is cooked.

Hyperbola

1. Orbital Trajectories: The paths of objects with sufficient energy to escape the Earth's gravitational field, such as comets and spacecraft, follow hyperbolic trajectories; this is important in space exploration.
2. GPS Systems: The orbits of GPS satellites form a pattern of hyperbolas as they transmit signals to receivers on the surface of Earth; the receivers can use the signals to determine their position accurately.
3. Radio Wave Propagation: Hyperbolic surfaces are used to model the propagation of radio waves emitted by a source; this is important in understanding and designing communication systems better.
4. Astronomical Studies: In binary star systems, where two stars orbit around a common center of mass, the light curve produced when one star eclipses the other often forms a hyperbolic shape.
5. Surveying and Navigation: Hyperbolic navigation systems, such as LORAN (Long Range Navigation), were used for maritime and aviation navigation before the discovery of GPS; these systems rely on the principles of hyperbolic positioning.
6. Mathematical Modelling: Hyperbolas are usually used in mathematical modeling and data analysis to describe relationships where one variable grows exponentially while another approaches a limit.

Conclusion

The world of conic sections presents us with unique shapes that have fascinated mathematicians and scientists for centuries. Parabolas and hyperbolas, while showing certain similarities, are fundamentally distinct due to their focal points, directrices, eccentricities, shapes, and asymptotic properties. Understanding these differences increases our knowledge of mathematics and our ability to appreciate the concept of parabolas and hyperbolas found in the universe of curves and shapes.