Square Root 1 to 100

The square root of a number is defined as the value that gives the number when multiplied by itself. The symbol utilized to represent the square root is denoted by √. This symbol is termed a root symbol. Determining the square root is straightforward when the number is a perfect square. However, the division method is utilized to find its square root when the number is not a perfect square.

Assume n as a positive number

√n.n = √(n)² = n

Features of the Square Root

Some of the significant properties of the square roots are as follows:

• If a number is a perfect square, then the perfect square root will also exist.
• If several zeros get attached at the end of a number, it will have a square root.
• The two square roots can be multiplied. For example, √5 × √3 the multiplication of these two root values will result in √15.
• The result will be radical numbers if two same square roots are applied. In other words, the outcome would be a non-square root number. For example, if √5 is multiplied by √5, the outcome resulting would be 5.
• Numbers that end in 2, 3, 7, or 8 (in the unit digits) do not have perfect squares
• The number could have a perfect square root when the number ends with 1, 4, 5, 6, or 9 in the unit digit.

Methods to Find the Square Root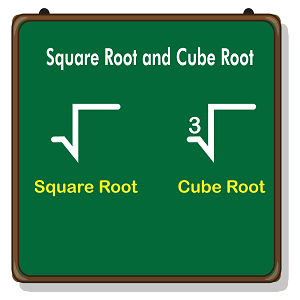

To find the square root of the given value, we need to determine whether the provided number is an imperfect or a perfect square. Suppose the number provided is 144, 169, 225. We can factorize such value with the factorization method. If we are given an imperfect square number such as 2, 3, or 5, then we have to take the long division method to determine the square root.

Given techniques are used to find the square root of the number:

1. Long Division Method
2. Estimation Method
3. Prime Factorisation Method
4. Repeat Subtraction Method

1. Long Division Method

Finding the square root of the given imperfect number is a bit complex. It is lengthy and time taking. Let's see one example.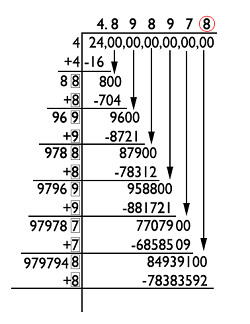

Thus, the square root of 24 is 4.898978.

2. Estimation Method

It is sometimes also considered an s method and determines the square root by judging the value.

The square root of 4 is two, and the square root of 9 is 3. To find the square root of 6, we can guess the value comes between 2 and 3.

But we need to verify which value is closer to the , i.e., 2 or 3. Let us calculate the square of 2.44 and 2.8.

• (2.44)² = 5.9536
• (2.6)² = 6.76

We can observe that the square of 2.44 is much closer to the square root of 6.

3. Prime Factorisation Method

It is one of the simple methods to compute the square root of a given number. Let us understand with some examples:

Number: 256

Primer factorization of the number = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2

Square root of √256 = 2 x 2 x 2 x 2 = 16

Number: 169

Prime Factorisation of the given Number = 13 x 13

Square root of √169 = 13

Number = 576

Prime factorization of the given number = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3

Square Root of √576 = 2 x 2 x 2 x 3 = 24

4. Repeated Subtraction Method

According to this method, if the provided number is a perfect square, we can figure out the square root by the following steps.

• Continuously subtracting consecutive odd Numbers from the provided value
• Subtract until the difference becomes the zero
• The number of times the provided number has been subtracted is the required square root

We learn better from the example; let's find the square root of 16

16 - 1 = 15

15 - 3 = 12

12 - 5 = 7

7 - 7 =0

The number of subtraction done here is 4 times; therefore, the square root will be 4.

Square Root Table 1 to 100