Prime Numbers

Those numbers, which are divisible exactly by itself and one, are called Prime numbers. They contain only two factors, the number itself and 1. Numbers that have more than two factors are called composite numbers. 2, 3, 5, 7, 11, and 13 are known examples of prime numbers. One is placed in the category of neither prime nor composite. One is regarded as a prime and composite number.

Brief History of Prime numbers

Eratosthenes discovered the prime number in 275-194 BC, Greece. He used the example of a sieve to explain the prime number from the natural number and filter out the composite number.

Properties of Prime Numbers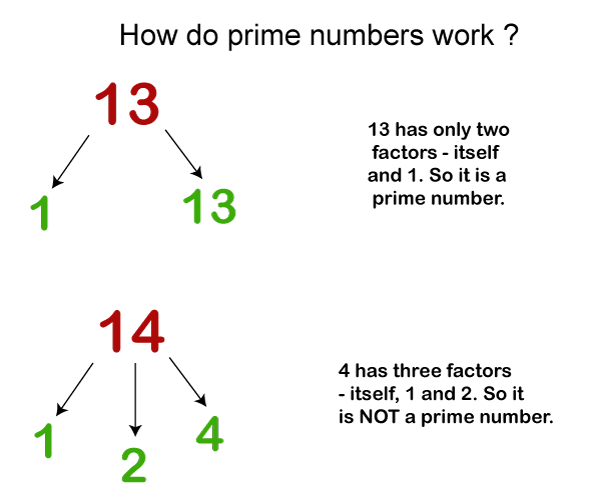

The properties of prime numbers are given below, and they are:

1. A number greater than one can be divided with at least one prime Number.
2. Even positive Numbers greater than two can be written as the sum of two primes.
3. Apart from 2, all prime numbers are odd. There is only one even prime number, i.e., 2
4. Two prime numbers will always be co-prime to each other.

Facts Regarding Prime Numbers

• Co-prime numbers: Numbers are regarded as a co-prime number when their highest factor is 1. Examples of co-prime numbers include 6 and 13, as they only have one as a common factor. Co-prime numbers and Prime numbers are not the same.
• Even Prime Numbers: Even prime number is 2, and other prime numbers are odd, which can be called an odd prime number.

How to Find a Prime Number?

The given method will help you to find whether the provided number is prime or not:

Technique:1

It is known to us that 2 is only the even prime Number and the consecutive two numbers which are prime are 2 and 3. the prime numbers can be expressed in the given form 6n+1 or 6n-1 (except the multiples of prime numbers such as 2, 3, 5, 7, … ). Here, n denotes a Natural number.

For Example

6(3) +1= 13

Technique: 2

There is a technique to know the prime Number for the numbers greater than 40, and the formula can be expressed as n2−n+41 where n can be 0, 1, 2……

For example

3x3 + 3 + 41=53

Difference Between Prime Numbers and Composite Numbers

Some of the difference between the prime and composite number is given below:

Prime Number

• A Prime Number contains only two factors
• The prime number can only be divided by one or the number itself: 2 can be divided by the numbers 2 and 1. Other examples include: 191, 181, 7, 11

Composite Number

A composite number contains more than two factors and can be divided by all the factors. For four examples: 1, 2, 4, and it is divided by all its factors. Other examples include 184, 114, 85, 15

Frequently Asked Questions

Question: Is a ten a prime number?

Solution: The answer is NO.

The number 10 has two factors, i.e.,1, 2, and 5, divided by all its factors. Hence it is not a prime number.

Question: What are the first ten prime number and their sum?

Answer: The first ten prime numbers include 2, 3, 5, 7, 11, 13, 17, 19, 23, 29

Calculation of the Sum

2 +3 + 5 + 7 + 1+ 11 + 13 + 17 + 19 + 23 + 29 = Sum

Total sum= 129

Question: Calculate the mean and mode of the first ten prime numbers.

Answer: We know that the first ten prime number includes 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.

We also know the formula for calculating the mean and the formula

Mean= Sum of all the values/ Total number of values

Mean= 129/10

Mean= 12.9

12.9 is the mean for the first ten prime numbers

The calculation for the median

2, 3, 5,7, 11, 13, 17, 19, 23, and 29 are the first prime numbers

The prime numbers are already arranged in ascending order.

Total terms = 10

Mean of the 5^th and 6^th term = Median

5^th term= 11

6^th term= 13

Calculation of median= (11+13)/2

= 24/2

=12

12 is the median for the first ten prime numbers.

Question: Let p be the prime number and then determine the number of factors for p2.

Solutions: We are known of the fact that p2 can be written in the form of

&p x p= p2. Therefore, the factors for the p2 would be (1, p, and p2).

Let us assume that p =3; then, factors for the p include 1, 3, and 9.

So, we can conclude that p2 contains three factors.

Question: Count the prime number between 1 and 50

Solution: The list of prime numbers that count between 1 and 50 are:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, and 47.

The total number that exists between 1 and 50 is: 15

Question: Find the twin prime from the given pair of numbers

(1, 2) (1, 3) (13, 19) (3, 5)

We are known of the fact that 1 is neither prime nor a composite number. So, we can ignore those numbers which contain the digit 1.

We also know that the difference between pairs of prime numbers is 2.

Therefore, the (3, 5) is a pair of prime numbers that has a difference.