Equivalent FractionsDefinitionIn arithmetic, an equivalent fraction is a fraction with the different numerator and the denominator but represents the simplified value of that fraction or proportion (part) of the whole. In other words, equivalent fractions are different fractions that we get after simplification of the fraction or after multiplying by the same number in numerator and denominator. For example, 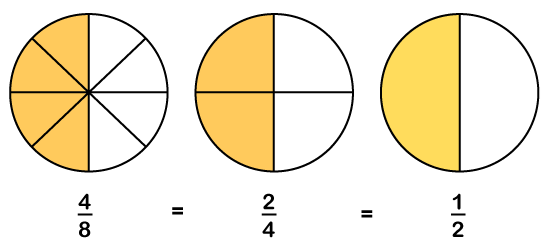
How to Find Equivalent FractionsThere are two ways to find the equivalent fractions:
Using MultiplicationIt is used when the fraction is in its simplest form. We multiply the numerator and denominator by the same number to get the equivalent fractions. For example, the equivalent fractions of 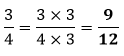
In the fraction 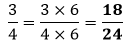
In the fraction Using DivisionIt is used when the fraction is not in the simplest form. We divide the numerator and denominator by the same number to get the equivalent fractions. For example, the equivalent fractions of 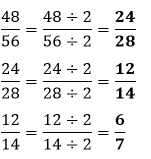
In the above example, we have divided the fraction by 2, to get the equivalent fractions. We have done this process until we get the simplest form of the fraction. The fractions that we get during the simplification are called equivalent fractions. 
Note: Never add or subtract the fractions to get the equivalent fractions. All equivalent fractions reduce to the same fraction in their simplest form. To get the equivalent fraction, it is not necessary to simplify the fraction in the simplest form.Equivalent Fractions ChartIn the following chart, we have covered some fractions equivalent that can help to simplify the fraction.
Let's see some examples. Example 1:Find the two equivalent fractions for each of the following fractions. 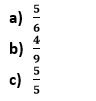
Solution: 
Example 2: Find the equivalent fraction of Solution: Let's divide the numerator and the denominator by 8 to get the equivalent fraction. 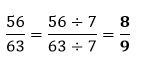

Example 3: Check the fractions Solution: 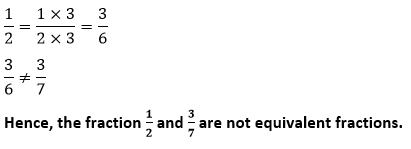
Example 4: Find the equivalent fraction of Solution: We have given that the denominator of the equivalent fraction is 21. Let the numerator is n, so the equivalent fraction will be 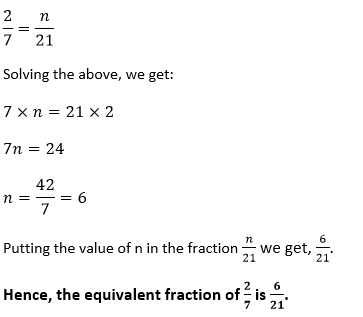
Example 5: Find the equivalent fraction of Solution: We have given that the numerator of the equivalent fraction is 15. Let the denominator is d, so the equivalent fraction will be 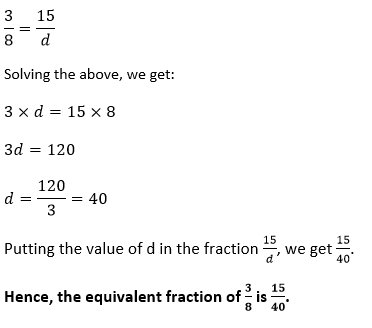
Next TopicSimplify Fractions
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share




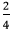 is equal to
is equal to 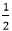 . Hence,
. Hence, 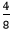 is also an equivalent fraction of
is also an equivalent fraction of 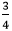 are:
are: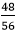 are:
are: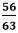
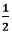 and
and 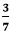 are equal or not.
are equal or not.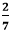 whose denominator is 21.
whose denominator is 21.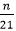 .
.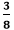 whose numerator is 15.
whose numerator is 15.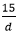 .
.




