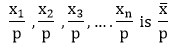Mean

Mean Definition

The mean in math can be defined as the sum of all observations in the distribution divided by the number of observations. The other definitions of the mean are: it is the average of the numbers or the sum divided by the count, is called mean.

It is also known as the arithmetic mean. It is denoted by x (read as x bar). The other types of the mean are Geometric mean and Harmonic mean, and weighted mean.

In statistics, the arithmetic mean is commonly used as the single value typical of a set of data. The arithmetic mean is also used in diverse fields such as anthropology, economics, and history. In economics, it is used to calculate per capita income (average income of a nation's population).

How to Calculate Mean

The calculation of mean is very easy. It is the same as finding the average.

• Sum up all the numbers
• Divide the sum by the number of terms

Mean Formula

OR

Where n is the number of terms, and ∑x_i is the sum of terms.

The above formula can be written as:

Where n is the number of terms.

Properties of Mean

• The sum of the deviations taken from the arithmetic mean is zero.
  If the mean of n observations x₁, x₂, x₃….,x_n is x then (x₁-x)+(x₂-x)+(x₃-x)…+(x_n-x)=0. In short, ∑ (x-x)=0
• If each observation is increased by p, the mean of new observations is also increased by p.
  If the mean of n observations x₁, x₂, x₃….,x_n is x then the mean of (x₁+p), (x₂+p), (x₃+p),….,(x_n+p) is (x+p).
• If each observation is decreased by p, the mean of new observations is also decreased by p.
  If the mean of n observations x₁, x₂, x₃….,x_nis x then the mean of (x₁-p), (x₂-p), (x₃-p),….,(x_n-p) is (x-p).
• If each observation is multiplied by p (where p≠0), the mean of new observations is also multiplied by p.
  If the mean of n observations x₁, x₂, x₃….,x_n is x then the mean of px₁, px₂,px₃,px_n is px.
• If each observation is divided by p (where p≠0), the mean of new observations is also divided by p.
  If the mean of n observations x₁, x₂, x₃….,x_n is x then the mean of
  

Let's see some examples that are based on the above formulas.

Example 1: Find the mean of the following values.

19, 28, 43, 74, 73, 16, 12, 3, 7

Solution:

Number of terms = 9

Sum of numbers = 19 + 28 + 43 + 74 + 73 + 16 + 12 + 3 + 7 = 275

We know that,

The mean of the given series is 30.55.

Example 2: Find the mean of the following values.

3, 6, 8, 12, 15

Solution:

Number of terms = 5

We know that,

The mean of the given series is 8.8.

Example 3: Calculate the mean of the following:

105, -67, 20, 45, 120, -55, 34, -2, -22, 27

Solution:

Number of terms = 10

We know that,

The mean of the given series is 20.5.

Example 4: The salaries of the employees are given, find the arithmetic mean of the salary.

5200, 5600, 2300, 7000, 2200, 4000

Solution:

Number of terms = 6

We know that,

The mean of salaries is Rs. 4383.33.

Example 5: The height of five students is 160 cm, 167 cm, 155 cm, 150 cm, 144 cm. Find the arithmetic mean of the height.

Solution:

Number of students = 5

According to the formula:

The mean of height is 155.2 cm.