Product in MathThe product in math is a term that refers to the result of a multiplication problem. In this section, we will learn the term product along with its properties and examples in detail. What is product in math?Product in math can be defined as the multiplication of two or more numbers together. In other words, an expression that identifies factors to be multiplied. The product is the result that we get on multiplying the two numbers multiplier and multiplicand together. 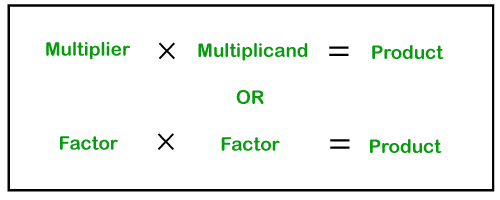
The number which is left of the multiplication sign is called the multiplier, and the number which is right of the multiplication sign is called the multiplicand. Both the multiplier and the multiplicand are also known as factor. How to Find ProductWe get the product of two numbers by applying the mathematical multiplication operation (× or * or .) between two or more numbers. For example: 9×7=63 Here, 63 is the product of 9 and 7. Similarly, 4×5×8=160 Here, 160 is the product of 4, 5 and 8. We can also find the product of two numbers by repeated addition method. It means add the number into itself up to multiplier times. This method applies only when we want to find the product of two small numbers.
a×b=b+b+b…+b
It means, add b up to a times or vice-versa. But it is not a traditional method of multiplying. For example, if we want the of 6 and 7, we can add the number 6 up to seven times. 6+6+6+6+6+6+6=42 Or 7+7+7+7+7=42 On multiplying the numbers 6 and 7, we get the same result. 6×7=42 Note: At the last of this section, we have written the steps of how to find the product of two 2-digit numbers and the product of two 3-digit numbers.Product of Two IntegersIntegers includes both positive and negative numbers. The multiplier or multiplicand may hold a positive or a negative sign before the number. No sign before a number represents a positive number. If the number holds a positive or a negative sign, they follow the rules, given in the following table. 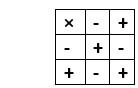
The above table represents that:
Let’s see some examples based on the above rules. Examples 15×5=75 -3×-9=27 -14×5=70 6×-12=72 Product of Two Decimal NumbersA decimal number is the number that contains a decimal point (.). For example, 23.56 is a decimal number. We can also find the product of two decimal numbers by using the following steps:
Example: Find the product of 23.3 and 12.21. Solution: In the question, there are two decimal numbers 23.3 and 12.21.
Product of Two FractionsFractions are the numbers that are in the form of numerator and denominator. To find the product of two fractions, multiply the numerator of the multiplier by the numerator of the multiplicand, and the denominator of the multiplier by the denominator of the multiplicand. In the terms of formula, we can write the above statement as: 

The product of a fractional number and its multiplicative inverse is always 1. Suppose, a fraction number is 
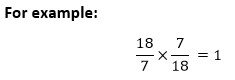
Always consider 1 if there is no denominator in the fraction. Digit 3 is same as 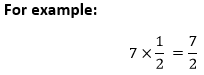
Sometimes, we need to simplify the fraction if the fraction is divisible by the denominator or the numerator of the multiplier is divisible by the denominator of the multiplicand or vice-versa. Note: The numerator and denominator must be divisible by the same number.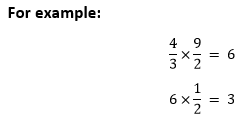
Product of Two Complex NumbersA complex number is a number that can be expressed in the form of (a+bi) or (a-bi), where a and b are real numbers and i is an imaginary number. 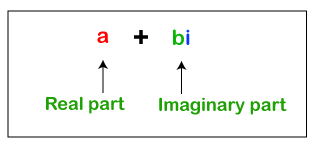
We can find the product of two complex number by using the distributive property. Remember the following points about i.
In general terms, the product of two complex numbers (a+bi) and (c+di) is: 
Let's see an example. Example: Find the product of two complex numbers (3-2i) and (-1+4i). Solution: (3-2i)×(-1+4i)=3×(-1)+3×(4i)-(2i)×(-1)-(2i)×(4i) Putting the value of i2=-1, we get: -3+14i-8×(-1) The product of two complex numbers (3-2i) and (-1+4i) is (5+14i). Product Properties of Square Root
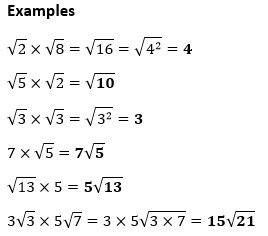
Properties of ProductThere are four basic properties of the product:
Associative Property When we multiply three or more numbers together, the product is the same regardless of which two are multiplied first. 
Commutative Property The order of multiplication does not affect the product. 
Identity Property We get the same number if a number is multiplied by 1. So, 1 is called the multiplicative identity. 
Distributive Property The property is known as the distributive property of multiplication over addition. It states that the sum multiplied by a number, we can multiply each piece of the sum by the number first and then add the results. 
Some other properties of the product are:
Product of Two Large NumbersOnce we catch the logic, then it is very easy to remember. For better understanding, we have written the steps of the multiplication of two large numbers. Note: The following methods apply when the multiplier and the multiplicand have the same number of digits.Product of Two Single-Digit NumbersTo find the product of two single-digit numbers, we must remember the tables or multiplication chart up to 10. It makes it easy to find the product of two numbers. Even we can find the product without using the pen and copy. The following chart shows the tables from 1 to 10. 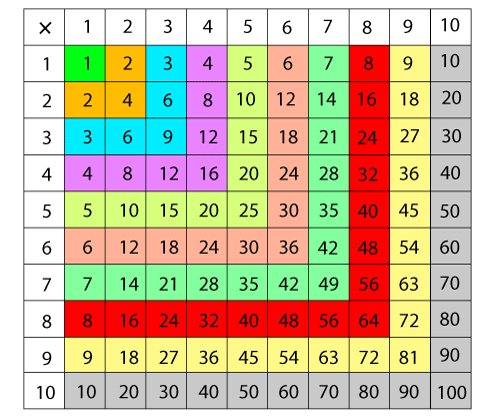
Product of Two 2-Digit NumbersIt includes three steps. Here, we have taken four alphabets (a, b, c, d) as a number for easy understanding. Suppose, we want the product of ab×cd, then we must follow the steps given below: 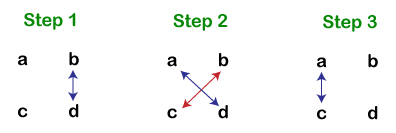
Let’s implement the above steps in an example. Example: What will be the product of 47×56? Step 1: (b×d) 7×6=42 Write 2 in the answer and take 4 as carry over to next step. (Updated Answer: 2) Step 2: [(a×d)+(b×c)]+carry over of the previous step if any [(4×6)+(5×7)]+4=63 Write 3 in the answer and take 6 as carry over to next step. (Updated Answer: 32) Step 3: (a×d)+carry over of the previous step if any (4×5)+6=26 Write 26 in the answer. (Updated Answer: 2632) The product of (47×56) is 2632. Note: Always write answer right to left.Product of Two 3-Digit NumbersIt includes five steps. Here, we have taken six alphabets (a, b, c, d, e, f) as a number for easy understanding. Suppose, we want the product of abc×def, then we must follow the steps given below: 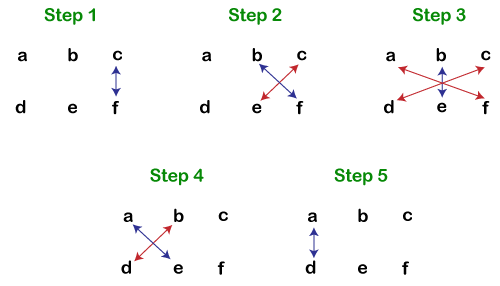
Let’s implement the above steps in an example. Example: What will be the product of 624×315? Step 1: (c×f) 4×5=20 Write 0 in the answer and take 2 as carry over to next step. (Updated Answer: 0) Step 2: [(b×f)+(c×e)]+carry over of the previous step if any [(2×5)+(4×1)]+2=16 Write 6 in the answer and take 1 as carry over to next step. (Updated Answer: 60) Step 3: [(a×f)+(b×e)+(c×d)]+carry over of the previous step if any [(6×5)+(2×1)+(4×3)]+1=45 Write 5 in the answer and take 4 as carry over to next step. (Updated Answer: 560) Step 4: [(a×e)+(b×d)]+carry over of the previous step if any [(6×1)+(2×3)]+4=16 Write 6 in the answer and take 1 as carry over to next step. (Updated Answer: 6560) Step 5: (a×d)+carry over of the previous step if any (6×1)+1=19 Write 19 in the answer. (Updated Answer: 19560) The product of (624×315) is 196560. Similarly, we can also find the product of two 4-digit numbers by using the following steps. 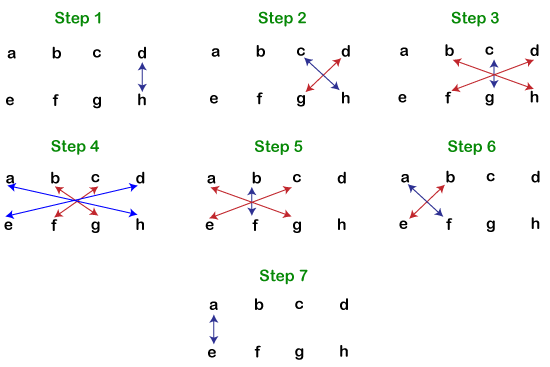
Next TopicFunction in Math
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





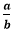 and its multiplicative inverse is
and its multiplicative inverse is 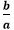 then:
then: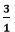 in the fractional form.
in the fractional form.




