of 100 and 120

In the field of Mathematics, numbers play a fundamental role in solving problems and understanding patterns; one such concept often used by us is the determination of the (GCF) greatest common factor between two or more than two numbers. In this article, we will get to know and understand the interesting concept of GCF, and after that, we will understand how to calculate GCF of 100 and 120; we will also get knowledge about the methods to find GCF and the applications of the greatest common factor.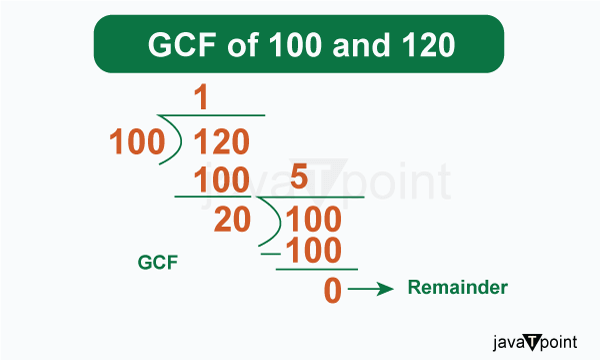

Understanding Greatest Common Factor (GCF)

The Greatest Common Factor (GCF) is the largest positive number that can divide those two or more numbers (without leaving any remainder), whose GCF we are calculating; GCF is also known as "Greatest Common Divisor (GCD)." It holds significant value in many mathematical fields, including algebra, number theory, and cryptography; the GCF is the foundation for simplifying fractions, solving equations, and calculating common factors.

Factors of 100 and 120

To find the GCF of 100 and 120, first, we have to find the factors of each number; a factor of a number is an integer that divides the numbers evenly and without any remainder.

• For 100: The factors are 1, 2, 4, 5, 10, 20, 25, 50, and 100.
• Similarly, the factors of 120 are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, and 120.

Determining the GCF

To find the GCF or GCD of 100 and 120, we need to see the common factors that are common (shared) in both numbers. As we know all the factors of 100 and 120, we can separate common factors, which are 1, 2, 4, 5, 10, and 20. But as per the name "greatest common factor," we are looking for the largest (greatest) integer from those common factors, which in this case is 20. So, the GCF (greatest common factor) of 100 and 120 is 20.

Methods to Find the GCF of 100 and 120

There are mainly three methods to calculate or find the greatest common factor of 100 and 120, that are:

1. Using Euclid's Algorithm
2. Long Division Method
3. Prime Factorization Method

1. Using Euclidean Algorithm

The Euclidean Algorithm provides an effective way to calculate the GCF of two numbers. According to the algorithm, GCF (X, Y) = GCF (Y, X mod Y), where X Y and "mod" represents the modulus operator.

Let's apply the Euclidean Algorithm to find the GCF of 100 and 120:

• Set X = 120 and Y = 100.
• Calculate GCF (120, 100) = GCF (100, 120 mod 100) = GCF (100, 20).
• Next, calculate GCF (100, 20) = GCF (20, 100 mod 20) = GCF (20, 0).
• Finally, GCF (20, 0) = 20 (since GCF (X, 0) = |X|, where X ≠ 0).

Therefore, the GCF of 100 and 120 is 20.

2. Long Division Method

The GCF of 100 and 120 can also be determined by the use of long division, by repeatedly dividing until the remainder becomes zero (0).

• Step 1: In this step, we will divide the larger number by a comparatively smaller number, i.e., we divide 120 (the larger number) by 100 (the smaller number).
• Step 2: Since the remainder is not 0, divide the divisor from step 1 (100) by the remainder (20).
• Step 3: Continue this process until the remainder becomes 0; at last, the divisor becomes the GCF of the numbers.

The divisor obtained in the last step, which is 20, represents the GCF of 100 and 120.

3. Prime Factorization Method

In this method, we first find the prime factors of each number. So, the prime factor of 100 is 2 x 2 x 5 x 5, and the prime factor of 120 is 2 x 2 x 2 x 3 x 5. Then we have to see and write the common factors from both the prime factors; as we can see that 2 x 2 x 5 is the common prime factor of 100 and 120. Therefore, the GCF of 100 and 120 is obtained by multiplying these common factors, which gives us 2 � 2 � 5 = 20.

Applications of GCF

The concept of GCF extends beyond simple arithmetic and finds applications in various real-world scenarios.

1. Simplifying Fractions: When we deal with fractions, finding the greatest common factor (GCF) of the numerator and denominator helps us to simplify the fraction, i.e., dividing both the numerator and denominator by their GCF reduces the fraction to its lowest terms.
2. Equivalent Ratio: In Mathematics, the ratio can be expressed as equivalent fractions; by finding the GCF of the terms in ratio, we can simplify it to its simplest form, which provides us a clear understanding of the relationship between the quantities that we are comparing.
3. Factorization: GCF plays an essential role in factorizing polynomials; by finding and factoring the GCF from the polynomial expression, we can break down those polynomials into simpler terms, making it easier to analyze and work with.
4. LCM: GCF is also important in determining the least common factor (LCM), which finds its applications in fields like scheduling, time management, and solving problems related to cycles or periodic events.

Conclusion

We can say that GCF of 100 and 120 is 20; by exploring divisibility, factors, and prime factorization, we all have better understood the concept of GCF. By gaining this knowledge, we get the opportunity to explore the field of Mathematics further and help in problem-solving in various fields; by sharpening our skills in finding the GCF, we can enhance our knowledge of Mathematics and unlock new skills in analyzing numbers.