What is a Zero Angle?

Using different shapes in a very specific manner in ancient structures can be seen as the beginning of 'geometry' as a methodology. The word's initial derivation comes from the Greek terms "ge" and "materia", which respectively mean "earth" and "measure."

The development of the contemporary world includes geometry as its basis. In addition, geometry is also a fundamental component of modern systems because it is used in planning, construction, engineering, the selection of building materials, and many other applications. It can also be used in a technological context for things like calculating different designs, production, making drawings, programming, etc.

The study of structures and their characteristics is the focus of the mathematic subdivision known as geometry. As essential parts of geometry, the study of angles and their different types based on their measurement is presented in the article. Beyond the five common angles, the article also explores the zero angle.

What do Angles mean?

Angles are the distance between two lines that intersect at a particular location or a point. They are made up of the vertex, which is the place where the angle develops, and the two arms, which are known as the angles' sides. Angles are expressed in degrees, with a range of 0° to 360°.

A shape or area known as an angle is created when two crossing rays come together. The Latin term "angulus", which means "a corner", is the source of the English word "angle". Carpus of Antioch proposed the first angle.

Types of Angles

Angles are categorized into various types based on how they are measured and rotated. They are classified into the following major types depending on the specific basis to be considered:

Angles on the Basis of Measurement

1. Acute Angle: The acute angle is any angle with a value less than 90°. It is always between 0 and 90, depending on the degree. When the rotation is anticlockwise, acute angles measure positively, and when it is clockwise, they are measured negatively.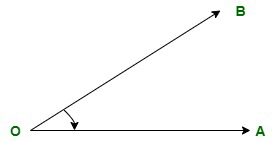

In the illustration, the angle's vertex, O, is formed by the intersection of two rays, OA and OB, and their angle of intersection, which is less than 90°, is formed at point O. An acute angle is a result because of this arrangement of lines.

2. Right Angle: A right angle is an angle that spans precisely 90 degrees. As half of 180 degrees form a right angle, it is also regarded as a half-straight angle. Depending on how the angle is rotated, the illustration of the angle may be positive or negative.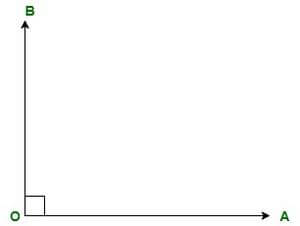

In the illustration above, the angle's vertex is represented by O, and the crossing lines OA and OB come together at point O to create a precise 90° angle. Consequently, AOB is a right angle.

3. Obtuse Angle: Obtuse angles fall within the range of greater than 90° and less than 180°. Any segment formed by intersecting lines, always between 90° and 180°, is an obtuse angle. If the movement is anticlockwise, the obtuse angle will be positive, and if it is clockwise, it will be negative.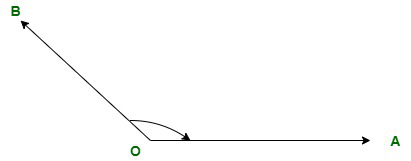

In the diagram, the angle's vertex is represented by O, and the crossing rays OA and OB that come together at point O to create the angle greater-than-90° angle are shown. AOB is, therefore, an obtuse angle formed by the intersecting lines as OA and OB.

4. Straight Angle: An angle is said to be straight when it covers precisely 180°. A straight line is formed by straight angles. Either positive or negative, it always represents a linear curve. Moving in a circular and anticlockwise direction will create a negative and positive linear (or straight) angle of -180° and 180°, respectively.

OA and OB are the two sides of the angle, and O is the vertex or place where these two arms meet in this illustration of a straight angle.

5. Reflex Angle: The reflex angle is the angle that is greater than 180 degrees but less than 360 degrees. Simply put, the degree is always within the range of 180° and 360°.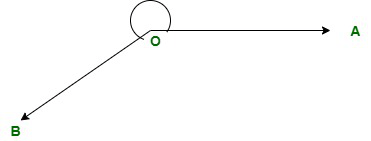

In the diagram, the angle's vertex is O, and the crossing rays OA and OB come together at point O to create an angle that is greater than 180 degrees. As a result, AOB is a reflex angle.

Angles on the Basis of Rotation

1. Positive Angles: A positive angle is one that is drawn from its beginning at the point (x, y) and proceeds anticlockwise from its base.
2. Negative Angles: A negative angle is one that is drawn from its beginning at the position (-x, -y) and proceeds clockwise from its base.

What is a Zero Angle?

When two lines are aligned with one another, a straight line is created. This angle is known as a zero angle. The two lines are parallel and at a 0° angle with one another. In the following illustration, two lines OA and OB are overlapping each other, starting from the vertex O. This arrangement of lines makes a zero angle between the lines.

Therefore, when two lines are aligned with one another, a unique kind of angle called a zero angle is created. A straight line is formed when two lines are aligned. However, this linear representation is not the same as pictures or diagrams drawn by straight angles. It can also be referred to as the exact opposite of a straight angle.

In geometry, angles are used to define forms and to calculate the magnitude of the angles that a shape's edges make. Straight angles, reflex angles, zero angles, acute angles, obtuse angles, and zero angles are all crucial examples of angles.

Uses of Zero Angle in Different Areas

Zero angles are significant in the study of geometry. Angles and their connections are crucial topics of trigonometry. Angles are used in trigonometry to quantify the measure of angles created by a triangle's edges. One of the angles that the edges of a triangular make is a zero angle. It is the angular relationship between two horizontal edges.

In mechanics, zero angles are used to specify a force's orientation. A push or draw that affects an item's position is referred to as a kind of work in physics. Angles are used to define the direction of work done because the force can be applied in various ways. Depending on the direction of the applied force, the work done can vary significantly.

In mathematics, the angle of overlapped lines on a graph is referred to as having zero angles. Four quadrants are created when a grid is made. The x-axis and y-axis decide which region is in which position. A line that is perpendicular to the x-axis or the y-axis is said to have a negative angle.

Navigation also makes use of zero angles. Angles are used to define a route's orientation on a map when navigating. The inclination of a path, when it is pointed in a straight line, is always zero.

Zero angles are also employed in building and engineering. Engineers use angles to make sure a structure is structurally solid when it is being built.

Conclusion

The idea of zero angles is crucial to the study of geometry, algebra, physics, mathematics, navigation, engineering, and building & construction. The angle of a line on a graph compared to a grid line, the angle of a route when it is guided along a straight line, and the angle of two lines when they are parallel while starting from the same point are a few arrangements that can be used to describe a zero angle. Zero angles are a basic idea in many branches of science and technology, and they are used in a variety of methods to define and quantify angles. Zero angles are often employed in construction to ensure that the structure is structurally safe and secure. Overall, understanding the concepts of zero angles is important for the knowledge of physics, mathematics and activities of daily living.