Geometric Shapes

We all must have heard the word 'Geometry,' which is considered a branch of Mathematics that deals with the study of angles, structures, shapes, and methods of their measurements, such as area and perimeter, number of sides, and angle between these sides; apart from these, this branch of mathematics also highlights the spatial properties of the shapes and structures and their relative configuration in a plane.

Geometry comprises two Greek words, 'Geo' and 'Metron.' The meaning of 'Geo' is 'Earth,' and 'Metron' is 'Measurement,' by this, we can say that Geometry is the part of mathematics that make us understand the measurement (area and perimeter) of shapes, objects, planets, angles, etcetera, and this list goes on.

Geometry is mainly classified into two types based on the dimensions of shapes.

1. Plane surface or Two-dimensional (2-D) Geometry
2. Plan Surface or Three-dimensional (3-D) Geometry

One basic and most important point, which is followed in both 2-D geometry as well as in 3-D geometry, is that all the shapes and structures which are studied in Geometry are formed from the points, rays, lines, and plane surfaces. Geometric Shapes are part of Mathematics that shows us how an object will look in 2-D and 3-D, so in this article, we will learn about some Geometric Shapes and their names with some of their properties, and we will conclude this article.

Types of Shapes

Based on appearance, shapes can be categorized into three parts; in this paragraph, we will discuss each category in detail.

1. Open Shapes
2. Closed Shapes
3. Definite Shapes

1. Open Shapes

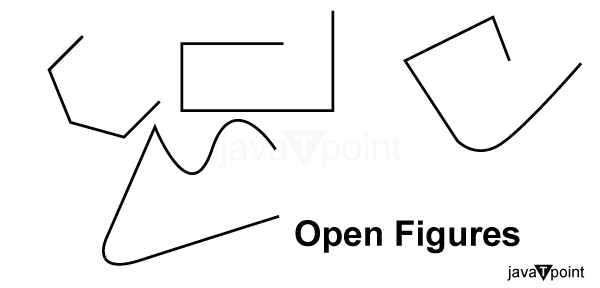
Open Shapes can be defined as incomplete shapes (apparent from the shape of that figure). They are shapes with different starting and ending points; they can be drawn by using lines and curves in a discontinuous manner.

2. Definite Shapes

All the shapes that have their particular name are called Definite Shapes. Shapes like triangles, rectangles, and squares are examples of shapes in 2-D and shapes like cuboids, cubes, and prisms are some examples of shapes in 3-D.

3. Closed Shapes

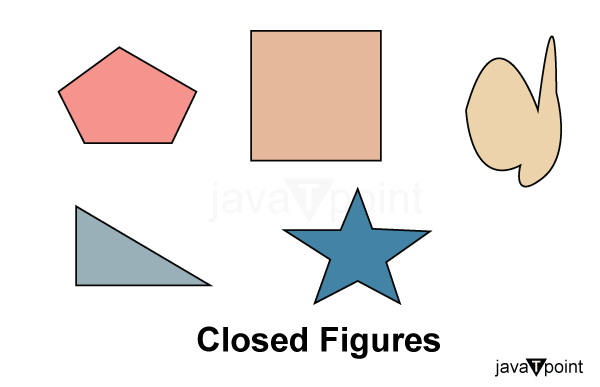
Shapes with the same ending and starting point are called Closed Shapes; all definite shapes are closed. Closed shapes can be formed by using lines and curves.

Two-Dimensional (2-D) Geometric Shapes

Two-dimensional (2-D) geometrical shapes are shapes that we can draw or see in two dimensions; for example: when we were children, we used to draw graphs on graph paper (graph paper that consists of a grid-like appearance); we can consider that graph as a two-dimensional plane. Some of the shapes which we can draw or see in a two-dimensional plane are discussed below:

1. Point: A Point is a basic geometric entity in a two-dimensional (2-D) plane; it represents a specific space location with no dimensions. If we pinpoint a point on the graph, it shows us the position of that point concerning the x-axis and y-axis.
2. Lines: When we join two points, a line is formed, or we can say that a line is a collection of all those points that lie on that line. In particular, a line has an infinite length, but a line segment has a definite length and two particular ends.
3. Polygon: Polygons are closed, flat 2-D shapes made of straight-line segments; at least three (3) line segments are needed to form a close shape, and that shape is called Triangle. As the number of sides increases in a closed shape, its name also changes; for example, if the number of sides of a polygon is six (6), we will call it a hexagon. The sum of interior angles in any polygon is always equal to (n-2) * 180 degrees, where n is the number of sides of that polygon.
4. Circle: A circle is a two-dimensional closed shape or surface which has no corners and no vertices, it can be defined as a path of points that are equidistant of a given point called the center of the circle, and the distance is called the radius of the circle. The area of a circle is given by the multiple of pi (π), and the square of the radius of the circle and the perimeter of the circle is given by twice the product of pi (π) and the radius, where π (pi) is a mathematical constant approximately equal to 3.14159.
5. Ellipse: Similar to a circle, an ellipse is also a two-dimensional (2-D) closed shape that has no corner and no vertices, but they have two centers (which are called foci) as they have two centers; they also have two different radii; one is called the major axis, and other is called the minor axis. The sum of the distances from any point on the ellipse to its two foci is constant, which makes the ellipse essential in various fields such as astronomy and engineering.
6. Curves: Curves are smooth and continuous shapes that lack straight edges; some examples of these curves are parabolas, hyperbolas, and sine functions; each of these curves has special properties that find applications in science and engineering.

Three-Dimensional (3-D) Geometric Shapes

Two-dimensional shapes lie on only the x-axis and y-axis, where the x-axis shows the length and the y-axis shows the object's width; in three-dimension (3-D), a new axis z-axis is also included that shows the height of that 3-D object or shape. Some of the shapes which we can draw or see in a three-dimensional (3-D) plane are discussed below:

1. Spheres: A sphere is a perfectly symmetrical three-dimensional (3-D) shape that can be defined as a closed 3-D shape that is equidistant from a given point; that point is called the center of that sphere, and the distance is called the radius of that sphere. We can also say that a circle is a shadow of a sphere.
2. Prism: We can say that a Prism is an upgraded version of a triangle, rectangle, or hexagon; when any of these shapes are considered as the base of a prism, and they are starched to a particular height, this becomes a 3-D shape, and that shape is called Prism.
3. Pyramids: Pyramids, on the other hand, have one base and triangular lateral faces that meet at a single vertex.
4. Cylinder: Cylinders are 3-D shapes with two parallel circles at the bottom and top, and a curved lateral surface connects both; this shape is called Cylinder. These shapes frequently appear in everyday objects like cans and bottles.
5. Cone: Cones have one circular base and a curved lateral surface that narrow to a single vertex. This shape we usually watch in Ice-cream cones and traffic cones.
6. Polyhedra: Polyhedra are three-dimensional solids with flat faces, straight edges, and sharp vertices. Regular polyhedra, like the tetrahedron, cube, cuboid, octahedron, dodecahedron, and icosahedron, have similar regular faces and symmetric structures. These shapes have fascinated mathematicians for centuries, showing beautiful structures and mathematical concepts.

Applications of Geometric Shapes in Real-World Scenarios

The applications of geometric shapes lie beyond mathematics, and geometric shapes play an important role in numerous practical applications in various fields, empowering innovations and advancement in science, art, engineering, and technology.

1. Architecture: In architecture, geometric shapes are the base of structural design, affecting everything from building layouts to the shapes of arches, domes, and columns. Regular polygons and symmetrical patterns create visually appealing and stable structures. Moreover, the principles of geometry are instrumental in urban planning, as they help design efficient road networks and optimize land usage.
2. Engineering: In engineering, geometric shapes are essential in designing machine parts, calculating the volume of materials, and analyzing stress and strain distribution in structures. Geometric principles guide the design of bridges, tunnels, and other critical infrastructure, ensuring safety and efficiency.
3. Computer Graphics and Animation: In computer graphics, geometric shapes form the basis for creating virtual 3-D models of objects, characters, and environments. Artists and animators use geometric shapes and algorithms to build complex 3-D scenes, apply textures, and simulate realistic physics.
4. Astronomy and Navigation: Geometric principles have played a significant role in astronomy and navigation throughout history; astronomers use geometric models to predict celestial events, calculate planetary orbits, and measure distances between celestial bodies (like Earth and Sun). Similarly, ancient navigators utilized geometric tools like astrolabes and sextants to determine their position at sea based on celestial observations (by observing the position of Stars).
5. Art and Design: Artists have long drawn inspiration from geometric shapes, including them in their artwork to create harmony, balance, and visual interest; from the intricate geometric patterns in Islamic art to the Cubist movement in the early 20^th century, geometric shapes have played a vital role in shaping artistic expression.
6. Biology and Molecular Sciences: In biology, geometric shapes find applications in understanding cellular structures, protein folding, and DNA organization. The study of crystallography, which deals with the arrangement of atoms in crystalline structures, relies heavily on geometric principles to determine the shapes of molecules and crystals.

Conclusion

The study of geometric shapes provides us with a window into the fundamental language of the universe, where mathematics and aesthetics converge from the limitless beauty of a circle to the intricate complexity of a polyhedron; these shapes hold unique properties that transcend cultural and temporal boundaries.

Throughout history, geometry has been crucial in advancing human understanding, influencing art, architecture, science, and technology. As we continue to explore the mysteries of the cosmos and unlock the secrets of the natural world, geometric shapes will remain an indispensable tool, enabling us to comprehend and appreciate the beauty and power of mathematics in our lives. Embracing the study of geometric shapes, we embrace the timeless pursuit of knowledge and the boundless creativity that emerges from the human spirit.