What is 10 to the Power of Negative 3?

Exponentiation in mathematics is the process of raising a base number to a certain power. The exponentiation 10 to the power of -3, in mathematics, is denoted by the symbol 10^-3. It involves taking the reciprocal of 10 cubed and decreasing the base number 10 to the power of -3. In this article, we will go into the relevance of 10^-3, examine the idea of exponentiation, and talk about numerous real-world scenarios where such small numbers are relevant..

What is an Exponentiation?

Exponentiation is a basic mathematical technique that enables repeated multiplication's simple and effective expression. The exponent, also known as the power, denotes how many times the base has been multiplied by itself. The base and exponent in 10^-3 are 10 and -3, respectively.

Negative Exponents

A negative exponent is the multiplicative inverse of the base raised to power with the opposite sign of the supplied power. In other words, a negative exponent indicates that we need to take the reciprocal of the base number and raise it to the positive power. For instance, (3/2)^-2 can rewritten (2/3)^2. We know that an exponent describes how many times a number has been multiplied by itself. For instance, 3^2 = 3*3. In the case of positive exponents, we simply multiply the base number by itself repeatedly. However, when dealing with negative exponents require us to multiply the base number's reciprocal by itself. For instance, 3^-2 is (1/3)*(1/3).

Rules of Negative Exponent

For negative exponents, we have a set of principles or laws that make the calculation simple. The fundamental guidelines for resolving negative exponents are listed below.

Rule 1: According to the negative exponent rule, given a base 'a' with a negative exponent -n, multiply the base's reciprocal (1/a) by itself n times.

For example, a^(-n) = 1/a * 1/a * ... * 1/a (n times) = (1/a)^n.

Rule 2: This rule also applies when the denominator has a negative exponent.

For example, 1/a^(-n) = a^n = a * a * ... * a (n times) = a^n.

How Can Negative Exponents Be Solved?

Simplify after converting negative exponents into positive exponents according to one of the following rules to solve equations with negative exponents:

1. a^-n = (1/a)^n
2. 1/a^-n = a^n

Calculation of 10 to the power of Negative 3

The following formula may be used to compute 10^-3

10^-3 = 1 / (10 × 10 × 10) = 1 / 1000 = 0.001

Hence, 10 to the power of negative three is equal to 0.001.

Let's examine some comparisons and situations in which this value is pertinent to understand the magnitude of 10^-3 better. Notably, 10^-3 represents one thousandth, as indicated by the prefix "milli-" in the International System of Units (SI). This prefix signifies a division into one thousand parts. 10^-3 fall within the category of small numbers and have significance when dealing with fractional quantities.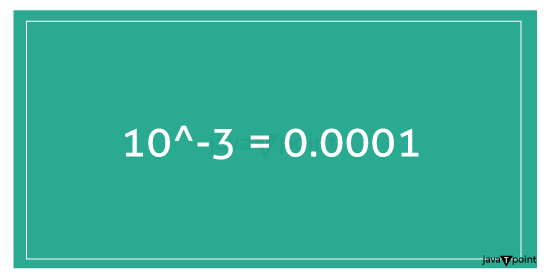

Negative Exponents are Fractions

The inverse of an integer is obtained when the exponent is negative. In other words, 5^-3 becomes 1/5^3, which equals 1/125. Similarly, for any integer a and a negative exponent n, a^-n can be expressed as 1/a^n. Negative exponents convert integers to fractions in this manner.

Uses of 10 to the Power (-3)

Let's look at a few examples of how 10^(-3)is used to indicate meaningful quantities:

Decimal Fractions: Small numbers are frequently represented using decimal fractions. To express that 0.001 is one part out of 1,000, it may be expressed as 1/1000. When working with exact measurements or computations, decimal fractions are crucial in chemistry, physics, and finance.

Probability: Small values are regularly found in statistics and probability. For instance, the chance of an event may be stated as 0.001, which denotes an extremely low likelihood.

Measurement Units: In the metric system, lengths are measured in millimeters (mm). It is equal to one-thousandth of a meter. This unit is widely used in engineering, manufacturing, and construction.

Conclusion

In conclusion, 10^-3 is an important mathematical notion that denotes the result of taking the reciprocal of 10 cubed. It is a tiny number with applications in measuring units, time intervals, scientific notation, decimal fractions, probability, and many other areas. The ability to comprehend tiny numbers and their exponential representation is essential for understanding a variety of facets of our environment, from precise measurements and computations to probabilistic occurrences and statistical analysis.