Simplify (1 - Sin x)(1 + Sin x)

For all conceivable values of the variables inside their respective domains, trigonometric identities are equations using trigonometric functions that are true.. These identities are derived from the geometric relationships and properties of right triangles, circles, and periodic functions. In this article, we will derive one such trigonometric identity by simplifying (1 - Sin x)(1 + Sin x).

What are Trigonometric Ratios

Trigonometric ratios are used to quantitatively connect the angles of a right triangle to the ratios of the lengths of its sides. Six fundamental trigonometric ratios exist in trigonometry: sine, cosine, tangent, cosecant, secant, and cotangent. These ratios are frequently represented by the abbreviations sin, cos, tan, csc, sec, and cot.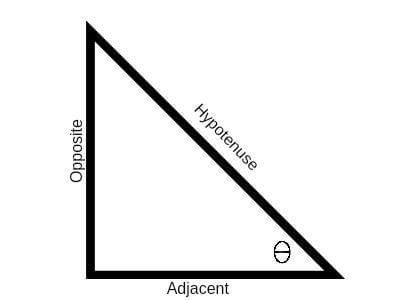

The sine function is denoted as "Sin" and is defined as follows: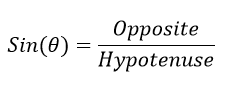

The cosine function is denoted as "Cos" and is defined as follows: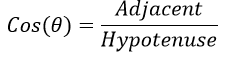

Here, theta represents the angle, and the opposite and adjacent sides refer to the sides of the right triangle relative to the angle.

What Is (1 - Sin x)(1 + Sin x)

Mathematically, we can say that:

(1 - Sin x)(1 + Sin x)= Cos² x

This identity provides a way to express the sine of an angle in terms of square of its cosine. It helps simplify trigonometric expressions by replacing the tangent of an angle with the cosine of the angle.

Explanation

To prove that (1 - Sin x)(1 + Sin x) is equal to Cos² x, we can start with the left side of the equation and manipulate it using algebraic identities until we arrive at the right side. Here's a step-by-step explanation:

• Step 1: Start with the left hand side of the identity:
  (1 - Sin x)(1 + Sin x)
• Step 2: Simplify the expression by using algebraic identity, (a + b)(a - b) = (a² - b²)
  (1 - sinx)(1 + sinx)= 1 -sin^2?x
• Step 3: Use the identity Sin² (x)+ Cos² (x) = 1 to rewrite the expression
  1 -sin² x=cos^2?2
• Step 4: Replace 1 -sin²?x with (1 - sinx)(1 + sinx)
  (1 - Sin x)(1 + Sin x)= Cos² x

Thus, we have proved that (1 - Sin x)(1 + Sin x) is equal to cos² x by stepwise manipulation of the equation.

Uses of Trigonometric Identities

The trigonometric identities are immensely useful in trigonometry, calculus, and physics.

• They can be used to solve trigonometric equations by transforming them into simpler forms. By substituting (1 - Sin x)(1 + Sin x) with Cos² x , equations can be rewritten in terms of a single variable for easier solving.
• Trigonometric identities aids in simplifying complex trigonometric expressions involving multiple angles. Repeatedly applying the trigonometric identities can reduce the number of angles and terms in an expression, enhancing clarity and facilitating further analysis.
• In calculus, trigonometric identities allow for the transformation of trigonometric functions into simpler forms. This simplification enables the application of integration and differentiation rules, helping to solve differential equations, evaluate integrals, and derive mathematical models in physics and engineering.
• Geometrically, the trigonometric identities help analyze angles and their relationships within shapes and figures. It allows for relating angles to their double angles, enabling exploration of symmetry, congruence, and similarity in geometric configurations.
• Trigonometric identities assist in solving problems involving angles in triangles, quadrilaterals, and other polygons.
• In physics, trigonometric identities are extensively used in wave mechanics, oscillations, and vibrations. It helps describe the behavior of waves, such as light and sound, by relating the angles of incidence and reflection.
• Trigonometric identities also play a crucial role in analyzing the phase difference between waves and determining interference patterns.

Conclusion

(1 - Sin x)(1 + Sin x)= Cos² x is a fundamental trigonometric identity that relates the sine function to the square of cosine of the angle. It serves as a powerful tool in trigonometry, calculus, and physics, facilitating the simplification of expressions, solving equations, and analyzing geometric and wave-related problems. Its versatility and wide range of applications make it an essential concept for anyone studying or working with trigonometry and its related fields.