Equation of a Circle

In geometry, a circle can also be represented in the expanded form. It is the result of expanding the binomial squares in the standard form and combining like terms. To find the equation of circle we use the distance formula.

In this section, we will learn the standard and general form of the equation of a circle, and also solve some problems based on it.

There are two forms of the equation of a circle:

• Standard Form
• General Form

Standard Form

If the equation of a circle is in standard form, we can easily find the center of the circle (h, k) and the radius of the circle. The standard equation of a circle is:

Where (h, k) is the coordinates of the center, and r is the radius of the circle. Remember that the value of r is always positive.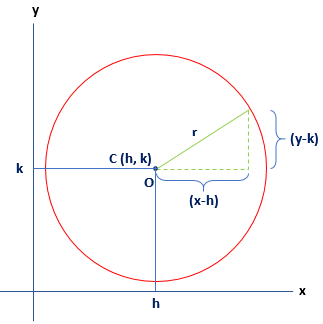

Let's see some examples based on the standard form.

Example 1: Find out the radius and center of a circle from the given equation. Also, draw the graph.

(x-2)²+(y-3)²=4

Solution:

The given equation is, (x-2)²+(y-3)²=4.

Remember: If the minus sign is preceding the (h, k), (h, k) will be positive.

Compare the given equation with the standard form, we get:

h=2,k=3 and r²=4
r=√4=2

Now, we can plot the circle on the graph paper with radius r = 2 and center (2, 3).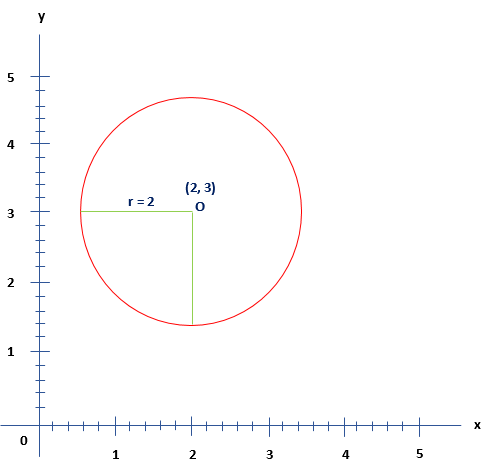

Example 2: Find out the radius and center of a circle from the given equation. Also, draw the graph.

2x²+2y²=8

Solution:

The given equation is, 2x²+2y²=8

The above equation is not matching with the standard form. So, first, we convert the equation in the standard form by dividing the equation by 2.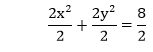

Solving the above equation, we get:

x²+y²=4

We can write the above equation as:

(x-0)²+(y-0)²=4

Compare the above equation with the standard form, we get:

h=0,k=0 and r²=4
r=√4=2

Now, we can plot the circle on the graph paper with radius r = 2 and center (0, 0).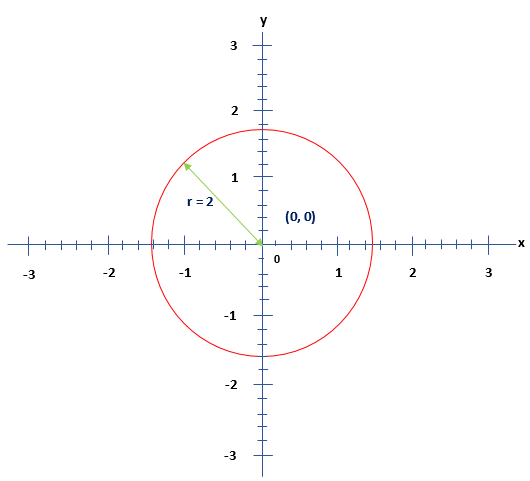

Example 3: Find out the radius and center of a circle from the given equation.

(x-4)²+(y+5)²=81

Solution:

The given equation is, (x-4)²+(y+5)²=81.

Compare the given equation with the standard form, we get:

h=4,k=-5

We see that y coordinate is negative. In general, y term is (y-k)². We have given that (y+5), so k must be negative. We can also write it as: (y-(-5))². Hence, y coordinate is negative.

Hence, the coordinate of the center is (4, -5) and the radius of the circle is 9.

r²=81
r=√81=9

Example 4: The radius of a circle is 25 cm and the center coordinate are (-2, 6). Write the equation of the circle.

Solution:

Given, radius (r) = 25 cm

Center coordinate (h, k) = (-2, 6)

(x-(-2))²+(y-6)²=25
(x+2)²+(y-6)²=25

Hence, the equation of the circle is (x+2)²+(y-6)²=25.

Example 5: Write the equation of the circle given below.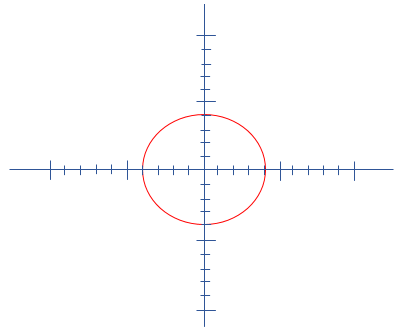

Solution:

In the given figure, the center coordinates (h, k) are (0, 0) and the radius (r) is 4. Hence, the equation of the circle is:

x²+y²=16

General Form

The general form of the equation is the expanded form of the standard equation. We know the standard equation of the circle:

(x-h)²+(y-k)²=r²…………(1)

Expanding the equation (1), we get:

x²+h²-2hx+y²+k²-2ky=r²

Rearrange the above equation, we get:

x²+y²-2hx-2ky+h²+k²=r²
x²+y²-2xh-2yk+h²+k²-r²=0…………(2)

Substitute the values of h, k, and r by the following values, we get:

h=-g,k=-f,c=h²+k²-r²

Put these values in the equation (2), we get:

x²+y²-2x(-g)-2y(-f)+c=0

Where (-g, -f) is the center of the circle, and the radius (r) is √g²+f²-c².

Where g, f, and c are constants.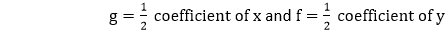

We can further substitute the values 2g, 2f, and c by D, E, and F, respectively.

Where D, E, and F are constants.

Note

• If the value of g²+f²-c²>0, the radius of the circle is real and the equation represents a real
• If the value of g²+f²-c²=0, the radius of the circle also becomes 0. In the particular case, the circle reduces to the point (-g, -f) and the circle is called a point circle.
• If the value of g²+f²-c²<0, the radius of the circle becomes imaginary. But the circle is not imaginary, it is real. This type of circle is called an imaginary circle.

Let's solve some examples based on general form.

Example 6: Find the center coordinated and radius of the circle from the given equation.

4x²+4y²-16x+24y-36=0

Solution:

The given equation is 4x²+4y²-16x+24y-36=0.

First, we will divide the whole equation by 4, we get: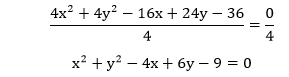

Rearranging the above equation, we get:

x²-4x+y²+6y=9……(1)

Now we will find the value of g and f, respectively.

We know that,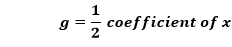

In the above equation, the coefficient of x is -4. Therefore,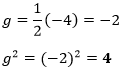

Similarly, we will find the value of f. We know that,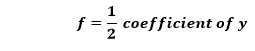

In the above equation, the coefficient of y is 6. Therefore,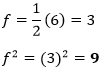

Note: We add the value of g² and f² to both sides of the equation.

Putting the value of g and f in the equation (1), we get:

(x²-4x+4)+(y²+6y+9)=9+4+9
(x-2)²+(y+3)²=22

Compare the above equation with the standard form, we get the center of the circle and radius of the circle.

h=2,k=-3 and r²=22
r=√22=4.7

Hence, the center of the circle is (2, -3) and the radius is 4.7.

Example 7: Find the center and radius of the circle from the given equation.

x²+y²+2x+4y-9=0

Solution:

The given equation is: x²+y²+2x+4y-9=0.

Rearranging the above equation, we get:

x²+y²+2x+4y=9
x²+2x+y²+4y=9……(1)

Now we will find the value of g and f, respectively.

We know that,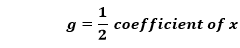

In the above equation, the coefficient of x is 2. Therefore,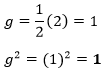

Similarly, we will find the value of f. We know that,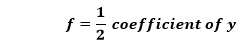

In the above equation, the coefficient of y is 4. Therefore,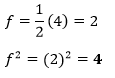

Note: We add the value of g² and f² to both sides of the equation.

Putting the value of g and f in the equation (1), we get:

(x²+2x+1)+(y²+4y+4)=9+1+4
(x+1)²+(y+2)²=14

Compare the above equation with the standard form, we get the center of the circle and radius of the circle.

h=-1,k=-2 and r²=14
r=√14=3.8

Hence, the center of the circle is (-1, -2) and the radius is 3.8.