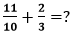AdditionIn arithmetic, addition is a type of basic mathematical operation. In primary education, students are taught to add numbers in the decimal system, starting with single digits and progressively tackling more difficult problems. In this section, we will learn the addition of two or more numbers. AdditionThe addition is a term used to describe to add two or more numbers together. In other words, it adds two or more numbers together. The number that is left and right of the plus symbol is called addend, and the number after the equal sign is called addition or sum. 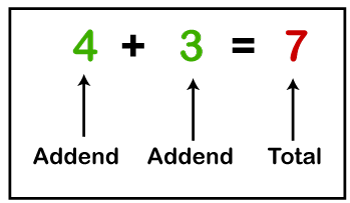
NotationA plus symbol (+) is used to denote the addition. It appears between the two numbers that are called infix notation. The other synonym of addition is added, sum, plus, and total. Sometimes it is also represented by the symbol ∑ (sigma). It is used when we have to add a large number. 
By using the plus symbol, we can perform addition between different numbers such as integers, real numbers, decimal numbers, complex numbers, etc. Besides this, it is also used in algebra to add vectors and matrices. For example, in the first basket, there are five apples, and in the second basket, there are 4 apples. If we count the apples of both the basket, we get 9 apples. 
In arithmetic, we can represent it in the mathematical expression as: 5+4=9 Addition Facts
Addition TableThe following table helps the children to memorize the sum of two numbers. You can find the sum of two numbers, between 0 to 10. 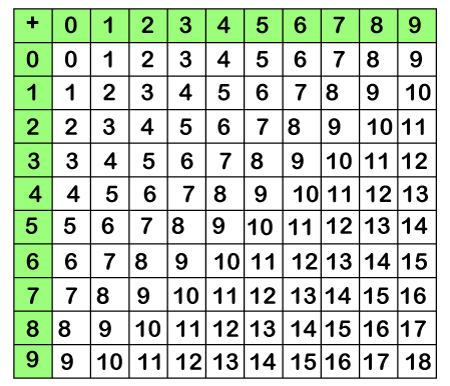
Before moving to the addition, we must be aware of the term carry. In arithmetic, a carry is a digit that is transferred from the right column to the left column and added to the transferred column. Addition of one-digit NumbersWe can find the addition of one-digit numbers with the help of the above table. Suppose we want to add 2 and 3 together. Search 2 in the left-most column, and 3 in the topmost row. In the current row, move down until you reach in front of the selected column. The square contains the addition of the numbers 2 and 3, i.e., 5. 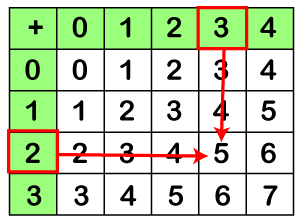
Similarly, we can find the sum of any single-digit number. Addition of Two-digit Numbers
Let's implement the above steps in an example. Example: Add 24 and 32. Solution: 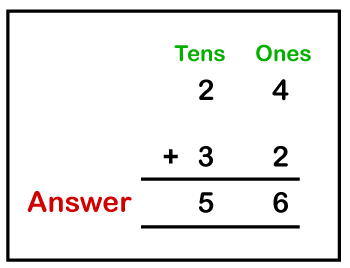
Example: Add 98 and 22. Solution: 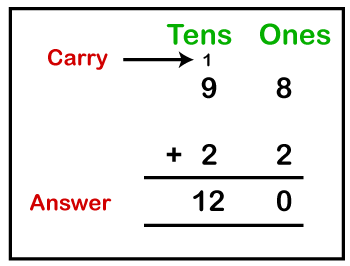
Addition of Three-digit Numbers
Let's implement the above steps in an example. Example: Add 367 and 492. Solution: 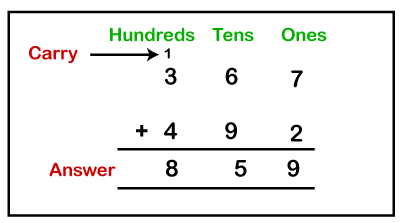
Example: Add 847 and 564. Solution: 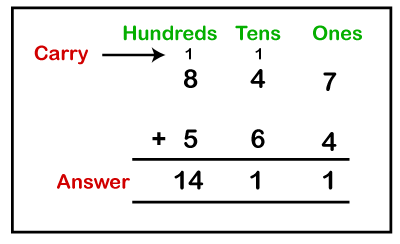
Similarly, we can add four-digit numbers, also. Addition of IntegersAn integer includes all positive and negative numbers, including 0. A number may have a positive or negative sign. The addition of integers with the sign follows the rules. Generally, we do not represent a positive number with + sign. In the following table, we have summarized the additional rule of positive and negative numbers. We have taken two numbers a and b as addend and z as sum.
Examples10+20=30 Addition of Decimal NumbersTo add two or more decimal numbers, follow the rules given below:
Example: Add 56.3457 and 2.4. Solution: 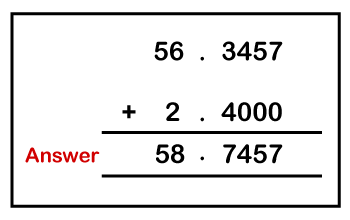
Example: Add 12.02 and 45.11. Solution: 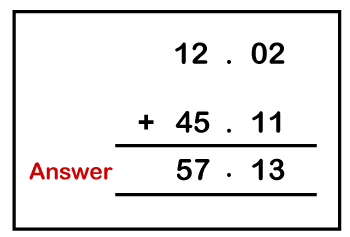
Example: Add 33.89, 0.0073, and 6. Solution: 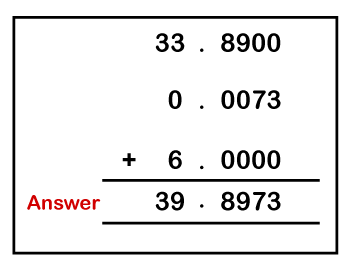
Addition of Rational NumberThe rational numbers are the numbers that are in the fraction form When the denominator of each fraction is the same:
In general, we can say that if 
Remember: To simplify a fraction, numerator and denominator must be divisible by the same number. Example: Find the sum of Solution: 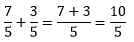
On simplifying the fraction Hence, the sum of When the denominator of each fraction is unlike (not similar):
In general, we can say that if 
Example: Solution: Let's solve the question according to the above steps. Find the LCM of the denominators. 
Divide the LCM by the denominators. 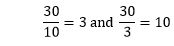
Multiply the resultant (from the above step) in the numerators, respectively, and simplify. 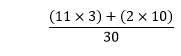
Add the numerators. 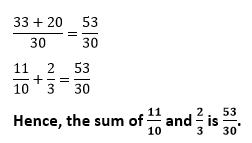
Addition of Complex NumbersComplex numbers are added by adding real and imaginary parts separately. In general, we can say that if a+bi and c+di are two complex numbers, then the addition of these numbers will be:
(a+bi)+(c+di)=(a+c)+(b+d)i
Example: Add (6+4i) and (5+3i). Solution: In the above example, 6 and 5 are real parts, and 4i and 3i are imaginary parts. So, we will add real parts together and imaginary parts together. (6+4i)+(5+3i)=(6+5)+(4i+3i) The sum of (6+4i) and (5+3i) is (11+7i). Example: Add (12+10i) and (7-9i). Solution: (12+10i)+(7-9i)=(12+7)+(10i-9i) The sum of (12+10i) and (7+9i) is (19+i)
Next TopicMedian
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share




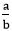 . Let's see how to add the rational number.
. Let's see how to add the rational number.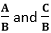 are two fractions, the addition of fractions will be:
are two fractions, the addition of fractions will be: .
.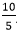 , we get 2.
, we get 2.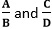 are two fractions, the addition of fractions will be:
are two fractions, the addition of fractions will be: