LCM of 10 and 70

What is LCM?

The least common multiple (LCM) is a mathematical concept to find the smallest common multiple of two or more numbers. The LCM of two numbers is the smallest positive integer divisible by both numbers wit.hout leaving a remainder. In our case, we want to find the LCM of 10 and 70, so we need to determine the smallest multiple that both numbers share.

Calculating LCM of 10 and 70

To continue, we might investigate several approaches to calculating the LCM. Each number's multiples can be listed until a common multiple is discovered. We can start by listing the multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, and so on. The multiples of 70 can also be listed similarly: 70, 140, 210, 280, 350, etc. Upon closer examination, we see that both integers have a common multiple 70. Thus, the LCM of 10 and 70 is 70.

For l numbers, however, this hand-listing technique becomes ineffective. Therefore, we may use more systematic approaches to get the LCM. Prime factorization is one such approach. We may find the LCM by dividing the numbers into their prime components and taking into account the maximum power of each prime factor.

Let's use prime numbers to factorize 10 and 70. 10 is equal to 2 * 5, while 70 is equal to 2 * 5 * 7. We consider the maximum power of each prime component to get the LCM. In this case, we observe the exponents of 2, 5, and 7, which are all raised to the power of 1.

Hence, the LCM of 10 and 70 is, 2*5*7 = 70

When calculating the LCM, the prime factorization technique offers a more organized and effective procedure, especially for bigger numbers with complicated components. It allows us to identify the prime factors and their highest powers, ensuring that the LCM is determined accurately.

Significance of Finding LCM

The LCM is useful in a variety of mathematical ideas and procedures. Fraction operations are a well-known use of LCM.

• We frequently need to identify a common denominator when adding or subtracting fractions. We can efficiently add and subtract fractions by finding the least common multiple (LCM) of the denominators. Consider the case when we want to add 1/10 and 3/70. The LCM of the denominators is 70. By converting both fractions to have a denominator of 70, we can add them together to obtain
  7/70 + 3/70 = 10/70 = 1/7
  The LCM helps ensure that fractions can be added or subtracted accurately and conveniently.
• The LCM is also used to solve problems and identify recurring patterns. For instance, the LCM aids in determining the fundamental unit of patterns involving periodic functions or cyclical phenomena, such as the behavior of waves or rotations. We can tell whether various cycles align or repeat by calculating the LCM of the cycle lengths.
• The LCM is a key tool in number theory for resolving modular arithmetic and divisibility issues. To uncover common divisors or finds connections between numbers, assists in identifying the least common multiple of two or more integers.

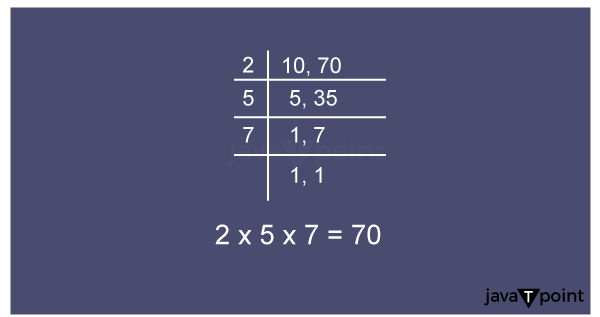
LCM Beyond Just Two Number

The term LCM can be applied to more than just two numbers. In this case, we can either employ the prime factorization approach previously stated or other methods like the "ladder" or "tree" method. These techniques entail methodically computing the LCM of several integers while considering their shared powers and factors.

Conclusion

In conclusion, finding the least common multiple (LCM) of two or more integers is aided by the LCM (Least Common Multiple), a fundamental mathematical idea. Despite being a straightforward example, the LCM of 10 and 70 shows how various computation techniques may be used, including manual listing and prime factorization. In addition, we explored the role of LCM in other branches of mathematics, such as number theory, equations, patterns, and fractions. The LCM is a useful tool for problem-solving and analysis because it sheds light on the connections and characteristics of numbers.