What is 25% of 100?

The percentage is a fundamental concept of mathematics that is not only important in Mathematics but also important in our daily lives. It helps us express fractions and proportions simply, making comparing and comprehending these values easier. One of the common examples that arise in many scenarios is calculating 25 percent, so, in this article, we will get to know the concept of 25 percent, understand the 25 percent of 100, and get to know the applications and conclusion in the end.

Understanding Percentage

Before we understand the calculation of 25 percent of 100, let us understand Percentages. Percentages are unique concepts that help us to express a portion or fraction of a whole as a fraction of 100. The word "percent" literally means "per hundred"; therefore, when we talk about 25 percent, it means 25 per hundred or 25 out of every 100.

What is the Actual Meaning of 25% of 100?

In particular, 25% of 100 is 25.

We can understand this concept by assuming 100 as 100 equal parts and objects and can assume anything; then 25 parts or objects from those 100 equal parts are considered 25%; for our case, 25 is the answer.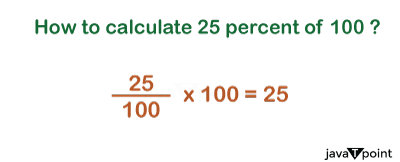

Steps to Calculate 25% of 100

We will learn how to calculate 25% of 100 with the help of some simple steps explained in the following lines.

Step 1. First, write the product of both numbers, i.e., 25% and 100, as shown below.

= 25% * 100

Step 2. As we know, the meaning of percentage is the 100^th part of a number or anything so we can replace the "%" with (1 / 100).

= 25% * 100 = (25 / 100) * 100

Step 3. Using the rules of multiplication and simplification, we get the following:

=25% * 100 = (25 / 100) * 100

= 2500 / 100

= 25

Suppose the whole pie chart represents 100 values. To determine 25% of 100, we calculate 25. The chart section occupied by the 25 values represents 25% of the total. The remaining portion of the chart represents 75% of the 100 values. Since 100 is the total value, the entire pie chart represents (whole) 100% of it.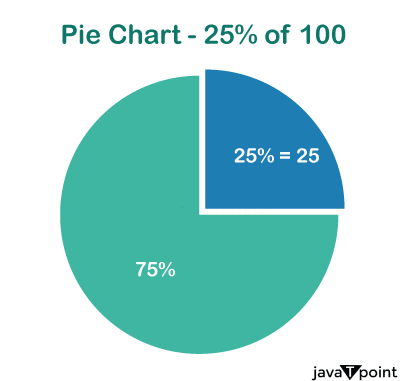

Applications and Examples

The concept of percentages and, specifically, 25% of 100 finds relevance in various real-life scenarios; let's explore a few examples to understand better its applications, which are discussed as follows:

1. Discounts: Imagine you are shopping during a sale, and an item you want is marked down by 25 percent; if the marked price is $100, the price after the discount will be $75. This example helps us understand how a 25 percent price reduction can help consumers save money.
2. Taxes: Taxes usually involve calculating percentages; for instance, if you give 25 percent of your income in taxes, and your income is $100,000, you would be required to pay $25,000 as taxes.
3. Grading Systems: In academic settings, percentages are frequently used to assess performance; if a test is worth 100 points, and you scored 25, you would have achieved 25 percent of the total marks.
4. Investment Returns: Investors usually calculate returns as percentages; suppose you invest $100 in a stock, and it generates a 25 percent return; your investment would then grow by $25, resulting in a total of $125.
5. Probability: Percentages are used in probability calculations; if there is a 25 percent chance of rain today, it means that out of every 100 similar weather situations, it would be expected to rain in 25.

Understanding 25% in Context

Viewing the percentage within the Context of the scenario or problems is essential. At the same time, 25 percent can also be represented as a quarter or the word we are more familiar with one-fourth (1/4) in a separate manner; its usage and importance can be changed based on the situation 25 percent is being used. A 25 percent increase in the world population is quite a significant increment, but on the other hand discount of 25 percent on an article is not as effective as it looked at in the above scenario.

Furthermore, understanding how percentages relate to other percentages is also worthwhile; for example, a 25 percent increase followed by a 25 percent decrease does not result in the original value; instead, it leads to a net loss of 12.5 percent. This illustrates the importance of comprehending and understanding the cumulative effect of percentages.

Some Solved Examples

Q. What is 25% of 20?

Solution:

Step 1. 25% * 20

Step 2. 25% * 20 = (25 / 100) * 20

Step 3. 25% * 20 = (25 / 100) * 20 = 5

Q. What is 18% of 50?

Solution:

Step 1. 18% * 50

Step 2. 18% * 50 = (18 / 100) * 50

Step 3. 18% * 50 = (18 / 100) * 50 = 900 / 100 = 9

Q. What is 75% of 40?

Solution:

Step 1. 75% * 40

Step 2. 75% * 40 = (75 / 100) * 40

Step 3. 75% * 40 = (75 / 100) * 40 = 30

What is 28% of 100?

Solution:

Step 1. 28% * 100

Step 2. 28% * 100 = (28 / 100) * 100

Step 3. 28% * 100 = (28 / 100) * 100 = 28

Q. What is 30% of 20?

Solution:

Step 1. 30% * 20

Step 2. 30% * 20 = (30 / 100) * 20

Step 3. 30% * 20 = (30 / 100) * 20 = 6

Conclusion

Percentages play a crucial role in everyday life by helping us to express fractions and proportions in a simplified manner. When we calculate 25% of 100, it equals 25. This means 25 is one-fourth (1/4) or a quarter of the value. Percentages, including 25%, are widely applicable in various scenarios, such as discounts, taxes, grading systems, investment returns, and probability calculations. By understanding percentages and their relationship to the whole, we gain valuable knowledge, interpret, and learn to apply percentages in our daily lives.