Parabola Graph

Quadratic function graphs are known as parabolas in mathematics. Pascal defined a parabola as a projective curve of a circle. Most of the time, physical body movements take a parabola-shaped curvilinear route. Projectiles falling with uniform gravity follow a path Galileo named the parabolic route.

Parabolas are plane curves with mirror symmetry that typically have a U shape. This chapter will outline the history of the standard parabola formula, show examples of the several standard forms, and describe the characteristics of a parabola.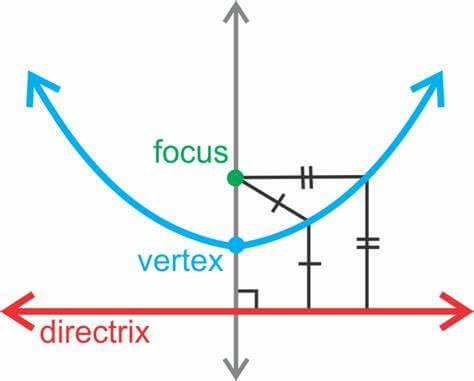

Introduction

A parabola equation has a point on the curve equally spaced from a fixed point and a fixed-line. The parabola's focus is the fixed point, and the directrix of the parabola is the fixed line.

Critical curves in coordinate geometry are parabolic curves. It's also crucial to remember that the fixed point is not located on the fixed line. The locations of points known as parabolas are those that are equidistant from a focus point and a particular line (directrix).

The formula for a Parabola

A parabola is typically defined as y = an (x-h)2 + k or x = a(y-k)2 + h, where (h,k) signifies the vertex. The formula y2 = 4ax defines a regular parabola.

To comprehend a parabola's components and characteristics, you should be familiar with the words below.

The point serves as the parabola's focal point (a, 0).

Directrix: A directrix is a hypothetical line drawn perpendicular to the y-axis and passes through (-a, 0). Parabolas with perpendicular axes are found in parabolas.

Focusing chord: A chord that runs through a parabola's center is referred to as a focal chord. At two places, this chord traverses a parabola.

Focal Length: The focal distance is the spacing between the focus and a point on the parabola with coordinates (x1, y1). The focal point is, as a result, at the same distance and perpendicular to the directrix.

Lacus Rectum: the chord that runs through the center of the parabola and is perpendicular to its axis. According to the formula LL' = 4a, the latus rectum length. The latus rectum's ends are (a, -2a), (a, -2a), and (a, a).

Eccentricity: (e = 1). It is the ratio of a point's distance from the focus to that of the directrix. When a parabola is taken into consideration, it equals 1.

Parabola's Standard Equations

For a parabola, there are four common equations. Four common shapes are depending on the parabola's axis and orientation. These parabolas have various transverse and conjugate axes. The four common equations and parabola forms can be seen in the following image.

From equations in their standard form, the following conclusions can be drawn:

• Regarding its axis, a parabola is symmetric. When the equation contains a term with y2, the axis of symmetry is along the x-axis; when it contains a term with x2, it is along the y-axis.
• When the axis of symmetry is along the x-axis, and the coefficient of x is positive, the parabola opens to the right; when it is negative, it opens to the left.
• Depending on whether the coefficient of y is positive or negative, the parabola expands either upward or downward when the axis of symmetry is along the y-axis.

Formula for Parabola

The Parabola Formula represents the general shape of a parabolic path in a plane. The formulas used to determine a parabola's parameters are listed below.

• The orientation of the parabola depends on the value of a.
• Vertex = (h,k), where k = f and h = -b/2a (h)
• Rectum Latus = 4a
• Focus: (1/4a, h, k+)
• y = k - 1/4a in the directrix

Parabola's Graph

Here is a parabola-shaped graph of the following quadratic equation. Take into account the formula y = 32 - 6x + 5. A, B, and C in this parabola are each equal to three.

When an is positive, the parabola is expanded.

Vertex: (h,k) (h,k)

h = -b/2a

= 6/(2 ×3) = 1

k = f(h) (h)

= f(1) = 3(1)2 - 6 (1) + 5 = 2

therefore vertex is (1,2)

Latus Rectum = (4a) = (4 + 3) = (12)

Focus: (1,25/12) = (h, k+ 1/4a)

The symmetry axis is x = 1.

Y = k-1/4a in the directrix

y = 2 - 1/12 ⇒ y - 23/12 = 0

Parabola's Characteristics

Here, we'll try to comprehend some key characteristics and vocabulary around a parabola.

Tangent: A line touching a parabola is known as a tangent. The equation yy1=2a(x+x1) is satisfied at the point of contact (x1,y1)(x1,y1) by a tangent to the parabola y2 = 4ax.

Normal: This line passes through the point of contact and the focus of a parabola and is perpendicular to it. The normal equation is (yy1)=y12a(xx1)(yy1)(xx1), travelling through the point (x1,y1)(x1,y1), and having a slope of m = -y1/2a for a parabola with the equation y2 = 4ax.

A cord of Contact: A chord of contact is drawn at the point where two tangents to the parabola are in contact. The equation of the chord of contact is yy1=2x(x+x1)yy1=2x(x+x1) at a point (x1,y1)(x1,y1) outside the parabola.

Pole and Polar: Draw a parabola's outer point-the location of the tangents' points of intersection-at the ends of the chords. The pole is defined as the polar drawn from this point. As a result, when the term "polar" is used, it refers to the pole. For a pole with coordinates of (x1,y1)(x1,y1), the equation of the polar is given by yy1=2x(x+x1)yy1, where y2 = 4ax for a parabola.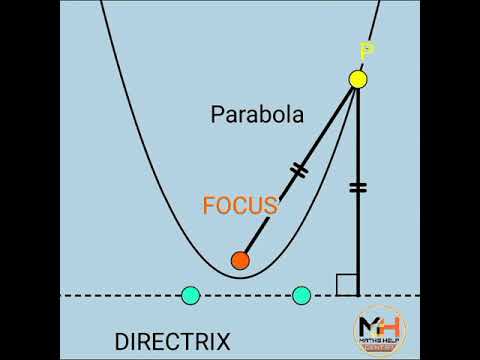

Coordinates in Parameters: A parabola equation's parametric coordinates are (at2, 2at). These coordinates represent all the points on the parabola.

The Conclusion

The smooth, U-shaped curve of an illustrative graph depends on the sign that its coefficient carries on whether it will expand upwards or downwards. The two points that make it simplest to graph a parabola are the better and the intercepted. The axis of symmetry is another tool utilized in graphing a parabola. The points on each side of this have the same value. You can also stay with other points on the graph if it has an x-intercept or a.