Surface area of a SphereIn this section, we will learn sphere definition, properties, and area of sphere formula along with examples in detail. SphereA sphere is a round shape solid object in three-dimensional space. It can be defined as the set of points that are all at the same distance form a given point (center). The perfect example of the sphere is the globe and ball. 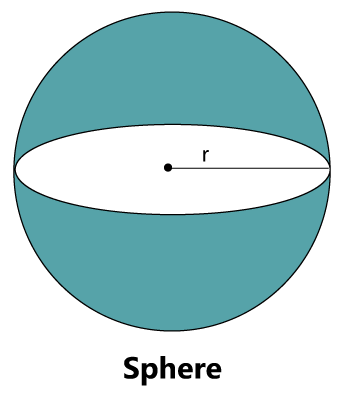
There is a slight difference between a sphere, and a circle is that a circle is a two-dimensional shape while the sphere is a three-dimensional shape. HemisphereIt is the half of the sphere. 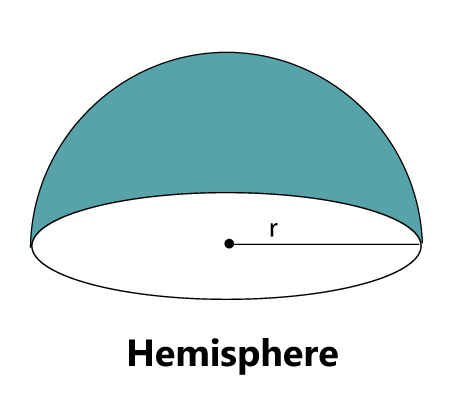
Properties of a Sphere
Surface Area of a SphereThe region covered by the surface of a sphere is called the surface area of a sphere. The surface area of a sphere is the same as the surface area of a cylinder with the same radius and height as the sphere. We can also say that it is four times the area of a circle.
Surface Area of a Sphere (A) = 4πr2
The surface area of a sphere in terms of diameter:
Surface Area of a Sphere (A) = πd2
Where d is the diameter. 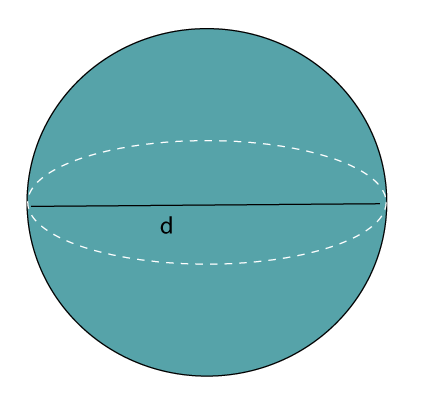
The area of a three-dimensional shape can be divided into three categories:
From the above points, we can conclude that:
Total surface area of a sphere = Curved Surface area of a Sphere
Surface Area of a Hemisphere
Surface Area of a hemisphere (A) = 2πr2
ExamplesExample 1: The radius of a sphere is 4.7 cm. Find the surface area of the sphere. Solution: Given, radius (r) = 4.7 cm We know that,
Surface Area of a Sphere (A) = 4πr2
Putting the value of r in the above formula we get: A = 4 * 3.14* (4.7)2 A = 4 * 3.14 * 22.09 A = 277.4504 sq. cm. The surface area of the sphere is 277.4504 sq. cm. Example 2: Find the surface area of a globe whose radius is 12 cm. Round the answer to the nearest hundredth. 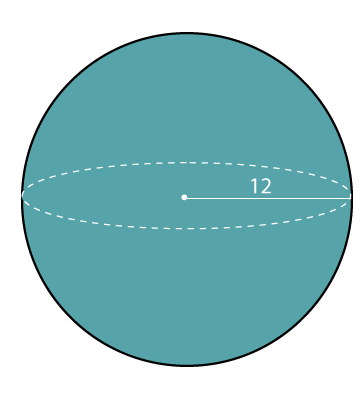
Solution: Given, radius of globe (r) = 12 cm We know that,
Surface Area of a Sphere (A) = 4πr2
Putting the value of r in the above formula we get: A = 4 * 3.14* (12)2 A = 4 * 3.14 * 144 A = 1808.64 sq. cm. The surface area of the sphere is 1808.64 sq. cm. Example 3: The radius of a hemisphere is 6.6 cm. Find the surface area of the hemisphere without the base. Solution: Given, radius of hemisphere (r) = 6.6 cm. 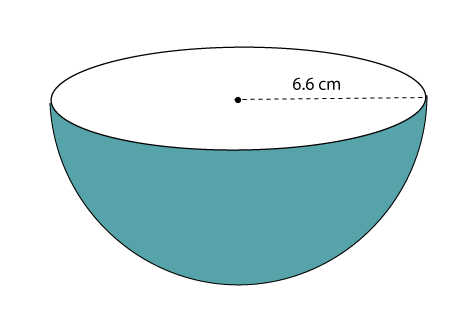
We know that,
Surface Area of a hemisphere (A) = 2πr2
Putting the value of r in the above formula, we get: A = 2 * 3.14 * (6.6)2 A = 2 * 3.14 * 43.56 A = 273.5568 cm2 The surface area of the hemisphere is 273.5568 cm2. Example 4: Find the surface area of the sphere whose diameter is 7 cm. Solution: Given, diameter of the sphere (d) = 7 cm. 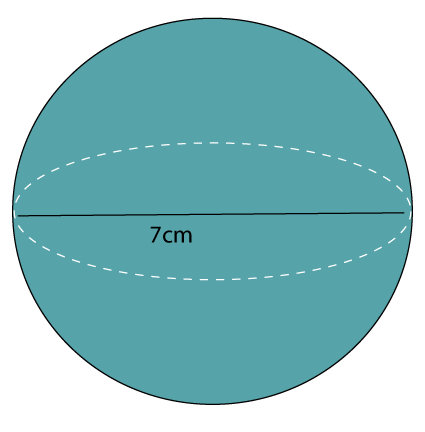
We know that,
Surface Area of a Sphere (A) = πd2
Putting the value of d in the above formula, we get: A = 3.14 * (7)2 A = 3.14 *49 A = 153.86 cm2 The surface area of the sphere is 153.86 cm2.
Next TopicHow to Find Standard Deviation
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









