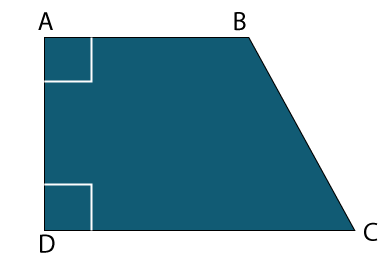
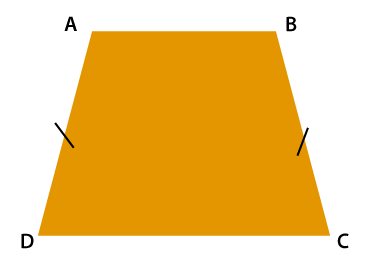
Area of trapezoidThe trapezoid is a convex quadrilateral shape. It means that a closed-shape that has four sides with one pair of parallel sides. In this section, we will learn how to find the area of a trapezoid. TrapezoidThe trapezoid is a gematrical shape that has four-sides in which a pair of opposite sides must be parallel is called trapezoid. The parallel sides are known as base, and the non-parallel sides are known as leg. The parallel sides can be horizontal, vertical, or slanting (diagonal). It is also known as trapezium. In the following figure, base1 and base2 are perpendicular to the dotted line, which represents the altitude (height). The altitude is perpendicular to the distance between two bases. 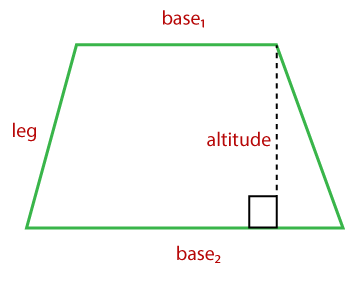
Properties of a Trapezoid
Types of TrapezoidThere are three types of trapezoid:
The different shape of trapezoid are: 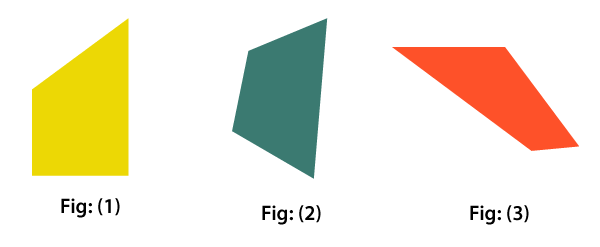
To find the area of the trapezoid follows the steps below:
Area of Trapezoid FormulaThe area of a trapezoid is the average width times the altitude. On implementing it in the formula: 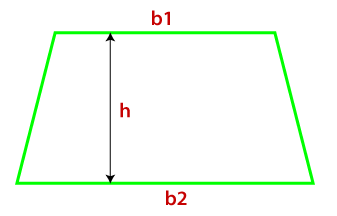
Area of trapezoid (A) = ½ (b1 + b2) * h
Or
Area of trapezoid (A) = h/2 * (b1 + b2)
Or
Area of trapezoid (A) = h * (b1 + b2/2)
Where b1 and b2 are the lengths of each base, and h represents the altitude. Derivation of Trapezoid FormulaLet's derive the formula by using the parallelogram from two congruent trapezoids.
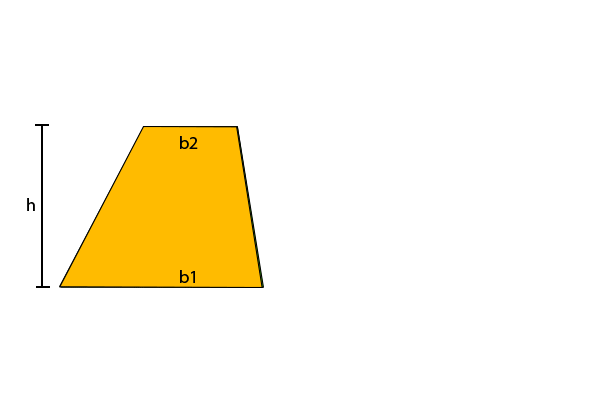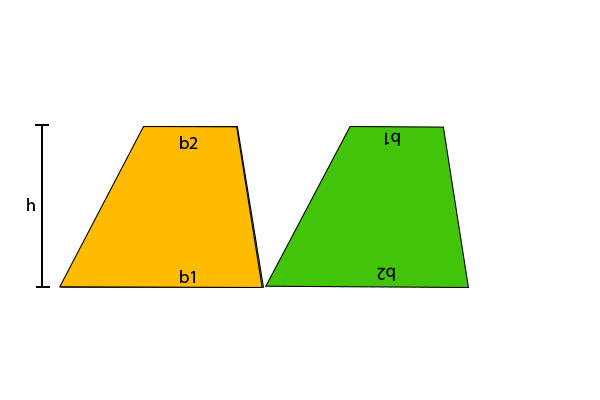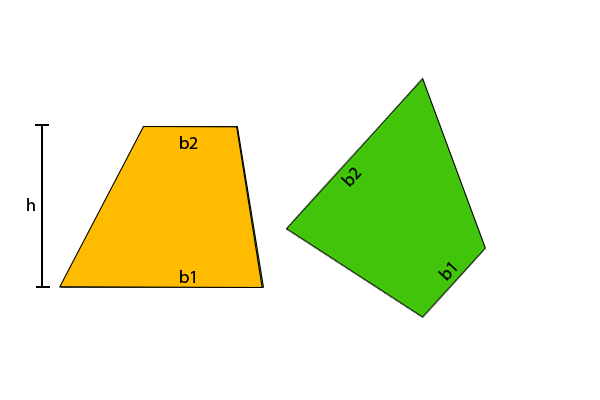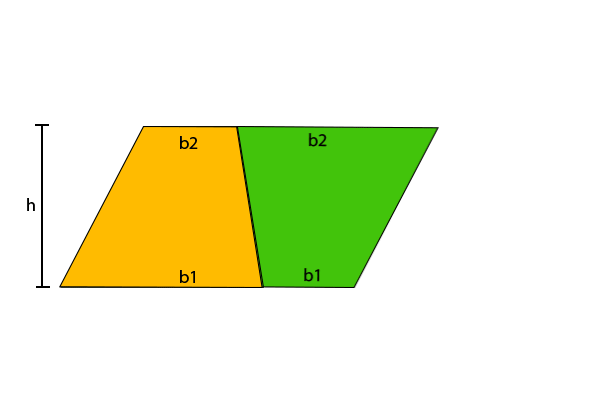
When we combine the two trapezoids (as above), it forms a parallelogram shape. The newly formed shape has two pairs of opposite congruent sides. We know that: area of a parallelogram (A) = b * h It means the area of a parallelogram is altitude (height) times the length of either base. From the above figure, the length of both the bases is equal to b1 + b2. According to the formula of the parallelogram, we get
A = (b1 + b2) * h
The above area is the area of two trapezoids. So, we need to divide it by 2 to get the area of one trapezoid. Area of trapezoid (A) = (b1 + b2) * h / 2 Arranging the above formula, we get:
Area of trapezoid (A) = ½ * h * (b1 + b2)
Another way to calculate the area of a trapezoid by dividing the trapezoid into two triangles. 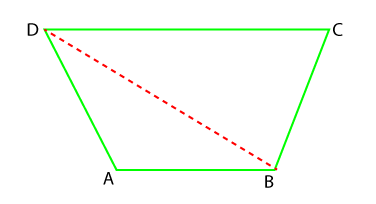
Now we have two triangles ∆ABD and ∆BCD. We will calculate the area of the triangles separately. The total area of the triangles will be the area of the trapezoid. 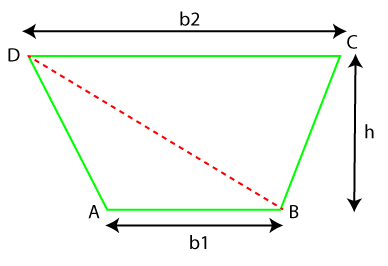
Area of ∆ A = ½ b1 * h Area of ∆ A = ½ b2 * h Adding the area, we get: A + A = ½ (b1 * h) + ½ (b2 * h) 2A = (b1 + b2) * h A = 1/2 (b1 + b2) * h ExamplesExample 1: If the bases of a trapezoid are 30 inches and 20 inches. The height of trapezoid is 4 inches. Find the area of the trapezoid. 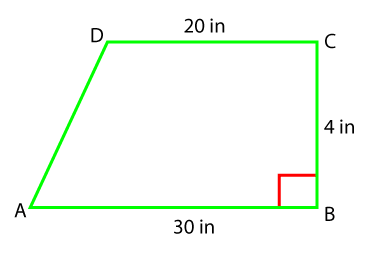
Solution: Given, b1 = 30 inches, b2 = 20 inches and height = 4 inches Area of trapezoid (A) = 1/2 (b1 + b2) * h A = ½ (30 + 20) * 4 A = ½ (50) * 4 A = 200/2 A = 100 in2 The area of trapezoid is 100 in2. Example 2: Find the area of the given trapezoid. 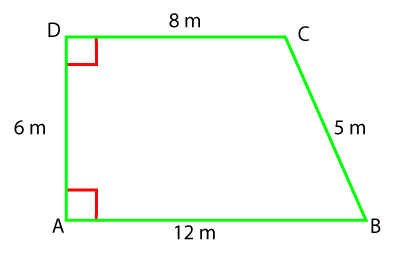
Solution: From the above figure, we will consider only parallel sides AB and CD because it makes the right angle with the parallel sides. Given, b1=12 cm, b2=8 cm and h=6 cm We know that, A = h/2 (b1 + b2) Putting the values in the above formula, we get:
A = 6/2(12 + 8)
A = 6/2 (20) A = 60 cm2 The area of the trapezoid is 60 cm2. Example 3: Find the area of a trapezoid whose bases are 10 m and 7 m, respectively. The altitude of the trapezoid is 5 m. Find the area. 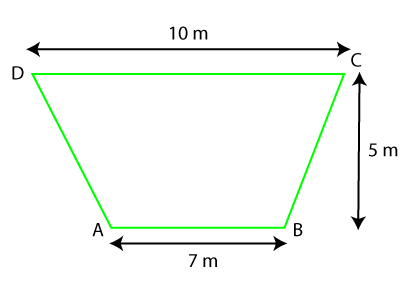
Solution: First, we will divide the trapezoid into two triangles, as we have shown in the following figure. 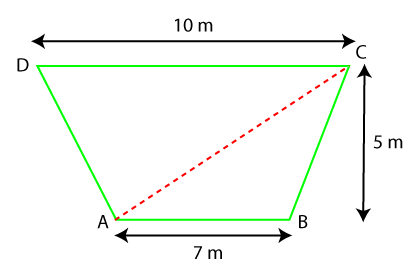
Now find the area of triangles separately. We know that: Area of triangle (A) = 1/2 b * h Area of ∆ABC = ½ (7 * 5) A = 35/2 A = 17.5 m2 Similarly, the area of ∆CDA = ½ (10 * 5) A = 50/2 A = 25 m2 Adding the area of ∆ABC and ∆CDA we get the total area of the trapezoid. Area of trapezoid = Area of ∆ABC + Area of ∆CDA Area of trapezoid (A) = 17.5 + 25 A = 42.5 m2 The area of the trapezoid is 42.5 m2.
Next TopicArea of Parallelogram
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share